Соотношения между параметрами нормированной [s,-jh] и ненормированной [вц] матриц имеют вид [2.1]

21 = 102/01 21н' 22 - 22н-

Для S-параметров Z01-Z02 и Sij=s,jH=S,j-.

2.4. СИСТЕМА УНИВЕРСАЛЬНЫХ s-ПАРАМЕТРОВ

Система универсальных s-параметров, введенная впервые в работе [2.2], является расчетной, т. е. системой, параметры которой не могут быть измерены непосредственно. Эти параметры, как и параметры нормированной матрицы рассеяния, описывают взаимосвязь падающих и отраженных волн мощности, но в отличие от последних являются универсальными, т. е. справедливыми как для вещественных, так и для комплексных нагрузок. Универсальные s-параметры позволяют найти, в частности, мощностные соотношения в транзисторах с согласующими четырехполюсниками, не прибегая к перемножению их матриц передач, s-параметры нормируются к действительной части комплексных сопротивлений генератора и нагрузки. Согласно [2.2], если

2 KiRe Z, I

21 Re I

(2.22)

(где Ui, /. - напряжения и токи на входе и выходе четырехполюсника, а Zi - комплексные сопротивления генератора (i=l) и нагрузки (i=2)), ai и fc,- имеют размерность (мощность) и представляют волны, падающие на четырехполюсник и отраженные от него (рис. 2.4). Связь й, и bi описывается в этом случае универсальной матрицей рассеяния волн мощности.

(2.23)

В матрице независимыми переменными являются Ci и Й2 - волны, падающие на четырехполюсник, а зависимыми bi и &2 - волны, отраженные от него. Отношения Ьг/щ суть коэффициенты передачи и отражения волн мощности.

На первый взгляд, может показаться непонятным, почему в этой матрице в качестве переменных выбраны 46

не токи или напряжения, а линейные комбинации этих величин. Однако нетрудно заметить, что квадрат модуля Ui равен максимальной мощности, отдаваемой генератором (и поглощаемой в нагрузке) в режиме комплексного согласования. Эта же величина представляет собой мощность, падающую на нагрузку, независимо от ее значения (рис. 2.5). Если Z*BZ то в нагрузке поглотится лишь часть падающей на нее мощности. Расчет с помощью (2.22) показывает, что эта мощность, т. е.

Рис. 2.4

Рис. 2.5

Re(L/,-/*i), равна разности квадратов модулей волн мощности:

fl,2 fc,2 Re(t;i/*i).

(2.24)

Отраженную мощность можно приписывать действию генератора с максимальной мощностью \bi\, посылающего отраженную волну bi. Таким образом, введение обобщенной матрицы волн мощности оправдывается возможностью отождествления и г| с мощностями прямой и отраженной волн *К Однако сами комплексные величины йг, Ьг И ИХ отношсния не допускают ясной физической трактовки, как квадраты их модулей**). Так, принимая за определение коэффициента отражения волн

*) Можно показать, что в общем случае, когда ReZ, может быть и отрицательной, а,Р, представляют собой обменные

мощности. При этом, если ReZ,<0, то aiP не равна максимальной мощности, отдаваемой генератором, поскольку последняя бесконечно велика, а aiP конечна.

**) Это следует не только из того, что на СВЧ измеряются мощности, а не напряжения, но главным образом из того, что все измерения в этом диапазоне выполняются с генераторами и нагрузками, сопротивления которых имеют активный (а не комплексный) характер.

мощности bjai отношение s,==(ZH-Z*0/(Z +Zi)

(2.25)

(это определение следует из (2.2) с учетом того, что /{= =UifZji), легко показать, что

(2.26)

Сравнивая (2.26) и выражение для обычно измеряемого на СВЧ коэффициента отражения (волн напряжения)

2н - Z Rk ~ i-h~~Ri

(2.27)

нетрудно заметить, что они отличаются в случае комплексного генератора и значение коэффициента отражения волн мощности можно лишь рассчитать. (Измерить

Si можно было бы, отнеся

а\ I-1 I-, реактивность генератора к

I hf; нагрузке и затем измерив

И' полученное сопротивление в

~.г| L линии с характеристическим

\)\ сопротивлением Zo=?,-).

LL-- Здесь уместно обратить

внимание на различие меж-Рис. 2.6 ДУ волнами, рассмотренны-

ми в § 2.2, 2.3, и волнами мощности, рассматриваемыми здесь (при комплексном внутреннем сопротивлении генератора и нагрузки). В первом случае входная и выходная линии согласованы с генератором и нагрузкой и отраженные волны в подводящих линиях являются лишь результатом включения четырехполюсника в линию. В последнем случае линия оказывается рассогласованной как с четырехполюсником, так и с генератором (и нагрузкой). Поэтому рассматриваемые здесь волны мощности характеризуют мощностные соотношения в терминах сосредоточенных постоянных четырехполюсника, но не характеризуют процессы в подводящих линиях. Так, если Zh=Z* вся мощность поглощается в нагрузке и отраженной волны (в терминах сосредоточенных постоянных) не возникает. Между тем в линии длиной itKl2, соединяющей генератор с внутренним сопротивлением Rг-]X, и нагрузку Яп-~]Х„ (при

В режиме дВуото/уоегв \ согласвВа/уия Гт

ЭТОМ в нагрузку поступает максимальная мощность), отсутствие отраженной волны в сечении аа (при R=Ri и Хг=-Х^ означает лишь интерференцию волн, отраженных от двух неоднородностей (рис. 2.6).

Далее покажем, что аналогичные трудности возникают при попытках измерения фаз коэффициентов передеч волн мощности. Однако и без этого ясно, что система параметров универсальной матрицы рассеяния, являясь мощным расчетным инструментом, не может рассматриваться как система рабочих параметров. Поскольку параметры универсальной матрицы волн мощности не могут быть измерены, важно найти соотношения, связывающие эти параметры с параметрами какой-либо рабочей системы.

В связи с этим рассмотрим соотношения, связывающие волны мощности с волнами напряжения или, что то же, параметры универсальной матрицы волн мощности со стандартными S-параметрами. Пусть четырехполюсник включен в разрыв не согласованной с генератором и нагрузкой линии так, что входное сопротивление генератора в плоскости входных клемм четырехполюсника составляет Zi, а в плоскости его выходных клемм Z2, и соответствующие коэффициенты отражения равны Ti и Г2 (рис. 2.7). Поскольку задачей является переход к системе S-параметров, т. е. к системе, в которой входная и выходная линии имеют одно и то же сопротивление, без уменьшения степени общности будем полагать, что Fi и Гг измерены в линии с одним и тем же характеристическим сопротивлением Zo.

Рассмотрев связь токов и напряжений на клеммах четырехполюсника с падающими и отраженными волнами мощности и напряжения, а также связь отраженных волн напряжения с падающими, можно получить более простые, чем на основании общей теории [2.2], [2.3], выражения:

4-384 49

в оВщем cffvae

Рис. 2 7

2V\Wzr\ 2KReZ,-

пад 1

(2.28)

Исключив из системы уравнений (2.28) напряжения и токи Vi, /,-, заменив их падающими и отраженными волнами С/щад. ftoTp и обозначив fi=2 l/ ReZi, Г,= = (Z-Zo) / {Zi-\-Zo), после преобразований получим

IOTP /,(1 Г*,)

2Г*1

/s.(l-Г*2) /г (1 - Г*2)

t/. p-S C/,, + S,.(/,,. 1;, р=5,.(/.д+5,А„.д- (2.29)

Изобразим указанные соотношения в виде ориентированного графа (рис. 2.8) [2.4]. Коэффициенты прямой

= S и обратной -

Cj=0

=S,j передачи, а также

коэффициенты отражения от входа

= S и вы-

= S. легко вычисляются по известным пра-

вилам [2.5] из представленного на рис. 2.8 графа. Минуя промежуточные выкладки, окончательно получаем

о, А*г [(1 - r,S ) (8гг - Г*.) + Г,5, А.]

5 11 -Л, [(1 -r.S.i) (1 -ГА2)-Г,ВДг5 ] Л%5.,[1-Г.П

Л, [(1 - r,S ) (1 - Г,5,Г) - r,r,S S ]

Л*,5 (1-Г.П

Лг [(I -r.S ) (1 -Т,8 )-ТгТ,8 8г]

(2.30)

(2.31)

(2.32)

S - [(1 - Г,5.,) - Г%) + r,s, А,] >1г [(1 -r,S ) (1 - rSs) - ТгТ,8 8~]>

(2.33)

где г,-(Zi-Zo)/(Z,-j-Zo)-коэффициенты отражения от входных и выходных нагрузок Z,- в плоскости транзистора в линии со стандартным характеристическим сопротивлением *) Zo=50 Ом;

7ПГг7[(1 - Г, Г) ;t=l,2 (генератор, нагрузка).

(2.34)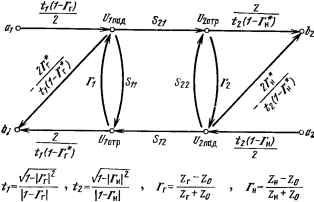

Рис. 2.8

В соответствии с выражением (2.32) реализуемый коэффициент усиления, выраженный через S-параметры,

-шм I l r,S -r,S,2-f Г,Г,Д| ( )

где A=SnS22-S12S21.

Фактический коэффициент усиления, т. е. номинальный при согласовании на входе

Ghomi=52iV(1-S ), (2.36)

) В общем случае, когда г^фТ-тф., (2.30)-(2.33) определяют связь между s-параметрами, измеренными с оконечными нагрузками Zi, и s-параметрами, измеренными с оконечными нагрузками Zj. В этом случае r,= (Zi-Zi)/(Z,-}-Z*,) - коэффициент отражения Zi от Z*, [3].

а номинальный коэффициент усиления (при согласовании на выходе)

G oM2=S2,/(l-S22). (2.37)

Для определения номинального коэффициента усиления при двустороннем согласовании Ghomi,2 необходимо найти условия, при которых коэффициенты отражения на входе Sii и выходе S22 равны нулю. Приравняв (2.30) и (2.33) нулю, получим, что условия двустороннего согласования сводятся к одновременному выполнению равенств

(2.38) (2.39)

2- i-r,s..

Нетрудно видеть, что r*i=rBx=Sii--Si2S2ir2/(1- -522Г2) - входной коэффициент отражения нагруженного четырехполюсника. Подставляя в (2.38) Г2=(Г*2)* из (2.39) и решая уравнение (ГОС*,-r*,5+Ci=0 относительно Г*1, находим решение системы в виде

l-ml 2С,

Г -Г В2±УВ2-4\С2 \ * г - тг -

где

Bi=l + SnP~S222-A2; 1=511-AS 22; B2==l+S222-SnP-A2; C2=S22-AS* 11;

(2.40) (2.41)

(2.42) (2.43) (2.44) (2.45)

индекс m означает согласование (match).

Из выражений (2.40), (2.41) следует отобрать решения, соответствующие 1Гг<1. Нетрудно показать, что, если Вг72Сг>1, одно решение больше, а другое меньше единицы. При этом ri и [Гг] меньше 1 при знаке -}- , когда В отрицательно, и при знаке - , когда В положительно. (При B,./2Ci<l оба решения равны единице и не удовлетворяют условию физического существования.) Таким образом, коэффициенты отражения от генератора и нагрузки (в плоскости транзистора) в режиме двустороннего согласования должны удовлет-

ворять условию Bi/2Cj>l и соотношениям (2.40), (2.41), где знак + относится к отрицательному В и - к положительному.

Следовательно, при двустороннем согласовании коэффициенты отражения от нагрузок Ti и Гг и S-парамет-ры связаны простыми соотношениями Г..,-Г2Д

1 - Г2522

522-Г,Д

1-r.S.,

(2.46) (2.47)

Воспользовавшись условием Bj/2Ci>l для предельного случая, когда Bi = 2Ci, и подставив сюда Bi и Q из (2.42) - (2.45), можно показать после необходимых преобразований, что это условие эквивалентно условию JOI, где

l-HA2 S 2 ,Sp

2IS.2IIS2.I

(2.48)

При К>1 действительные части входной и выходной проводимостей положительны (Вг > 2Ci), и двустороннее согласование транзистора возможно. К=1 является предельным случаем, при котором еще возможно согласование (поскольку при этом Bj=2C,. и ri=l). При К<1 входная и выходная проводимости транзистора становятся отрицательными, а его согласование невозможным. Коэффициенты отражения, определяемые выражениями (2.40), (2.41), будучи подставленными в (2.35), позволяют найти номинальный коэффициент усиления при двустороннем согласовании *).

С„о„... = IСI = 171 -VKl). (2.49)

Более простой вывод этого выражения приведен в § 11.4. Применяя для вычисления GnoMi,2 транзистора с теми же параметрами (2.49) и (2.14) и учитывая равенство IS21/S12I -у21/У12, убеждаемся, что значения К в этих выражениях равны. Постоянную К, инвариантную выбору матрицы параметров, с помощью которой она определяется, называют инвариантным коэффициентом устойчивости и широко используют при расчете устойчи-

. Аналогично G , . 2оГг, = S, р = S,2/S2, (К - VK - 1) -номинальный коэффициент передачи в обратном направлении.

вости транзисторных усилителей СВЧ. Здесь лишь заметим, что в безусловно устойчивом усилителе К должно быть больше единицы. Однако это условие еще не является достаточным.

2.5. СИСТЕМЫ НЕСТАНДАРТНЫХ S-ПАРАМЕТРОВ

Известно, что усиление СВЧ транзисторов падает с увеличением частоты и в рабочем диапазоне невелико.

Поэтому выбор входных (Zi-Zm\) и выходных (Z2=Zms)

нагрузок, обеспечивающих режим двустороннего согласования с целью предотвращения потерь на отражение , является весьма актуальной задачей. В других случаях важными параметрами являются сопротивления генератора Z\ и нагрузки Zg, реализующие коэффициент усиления, отличный от того, который получается при двустороннем согласовании. Упомянутые комплексные сопротивления и соответствующие им комплексные коэффициенты отражения (Гть Гтг при двустороннем согласовании, Гь Гг в общем случае) могут быть рассчитаны на основании измеренных значений традиционных S-параметров. Однако погрешности измерения традиционных S-параметров (они могут быть особенно велики при Sn и S22 близких к О или 1) приводят часто к существенным ошибкам при определении сопротивлений внешних нагрузок и, как следствие, к уменьшению коэффициентов усиления в реальных усилителях. Поэтому имеет смысл ввести систему параметров, свободную от указанных недостатков.

Непосредственное измерение коэффициентов отражения нагрузок Гтеь Гт2 ИЛИ комилексно-соиряженных с ними величин Г22т=Г*те2 (предстзвляющих собой входные и выходные коэффициенты отражения транзистора, нагруженного на нагрузки, реализующие режим двустороннего согласования, рис. 2.7) позволяет исключить погрешности, возникающие при расчетах с неточно измеренными стандартными S-иараметрами. Однако значение Гцт, Гггте для описания транзистора как четырехполюсника недостаточно; для этого необходима дополнительная информация в виде коэффициентов передач S12, S21 четырехполюсника, нагруженного на стандартные 50-ом-ные нагрузки.

Впервые введенная в [2.6] система, названная автором системой нестандартных S-параметров: Тцт, Ts-w, S21, S12 р общем случае Гь Г?, S12, Sji) позволяет осу-54

ществить однозначный переход к системе традиционных S-параметров Это очевидно, поскольку систему уравнений (2.38), (2.39) можно всегда разрешить относительно традиционных S-параметров.

Заметим, что при реализации режима двустороннего согласования нагрузки на клеммах четырехполюсника однозначно определяются через его параметры. Следовательно, входные сопротивления (и входные коэффициенты отражения Гц , Г22т) также можно рассматривать как собственные параметры четырехполюсника.

Для удобства измерений систему нестандартных параметров в предложенном симметричном виде следует усовершенствовать, чтобы отказаться от измерения фазовых углов коэффициентов передач. При этом система будет иметь вид

Г Г

is , is;7i, <р,.->...

в таком несимметричном виде система нестандартных параметров более удобна для измерений, поскольку при разностных измерениях фаз исключаются ошибки, возникающие при калибровке, т. е. при определении отсчетных плоскостей. Второе достоинство разностных измерений заключается в том, что они не зависят от неоднородно-стей измерительного тракта, если последний не обладает невзаимными свойствами [2.1].

При переходе от нестандартных несимметричных S-параметров к традиционным в результате расчета появляется неоднозначность в определении знака ф21+ф12-Для устранения неоднозначности требуется знать каждую фазу в отдельности, тогда формально несимметричные S-параметры сведутся к симметричным. Тем не менее системы неадекватны, поскольку для устранения неоднозначности нужны не точные, а лишь приближенные значения фазовых углов (чаще всего известные из общих представлений и предыдущего опыта). Однозначный переход к системе традиционных S-параметров, если нестандартные S-параметры получены в несимметричном виде, осуществляется по соотношениям, приведенным в [2.6].

Как уже упоминалось, система нестандартных S-параметров содержит неиосредственную информацию о коэффициентах отражения, необходимых для реализации режима двустороннего согласования. Другой важный параметр - инвариантный коэффициент устойчивости -

имеет простую связь S-параметрами:

i + is;pis;; p

2is;riis;ri

с измеренными нестандартными

(2.50)

где S;; = S;7S /S,J.

Выигрыш в значении погрешности, получаемый при измерении нестандартных S-иараметров (вместо традпционпых), нагляднее всего продемонстрировать на конкретном примере типичного транзистора. Пусть его традиционные S-параметры составляют: Sii = =0,335, Фи=2,46; S,2=0,11, %2=1,14, S2i = l,54, ф21=0,95, S22 =0,73, ф22=-0,55. Расчетные величины для этого прибора: К= 1,042, Gbomi,2= 10,285, 2вх=0,098Н 0.307, 2вых=0,507+] 3,58.

Максимальные значения погрешностей измерения традиционных S-параметров (зависящие от значений этих параметров и рассогласования оконечных нагрузок Г [2. 7]) при Г|=0,05 равны:

ASiimax=0,068, Дфп max=0,26, ДIS22I max=0,15, Дф12тах= =Дф21тах=0,0615.

Точность измерения модулей коэффициентов передачи примем равной 0,2 дБ. Можно показать, что лишь из-за неточного измерения Sii значение К, рассчитанное с помощью традиционных S-параметров (см. (2.48)), даст неправильную информацию о том, что усилитель потенциально неустойчив, а его двустороннее согласование невозможно. В наихудшем же случае расчетное значение К при указанных погрешностях измерения S-параметров составит 0,48. Можно показать, что в системе нестандартных S-параметров (при той же точности измерения модулей) К находится в предела? 1,03-1,05, а максимальный разброс измерения не превышает +0,01.

Заметим здесь, что при практической разработке усилителей иногда можно ограничиться измерением коэффициентов отражения Тцт, Тпт и модулей коэффициентов передачи \ S , S ,а для расчетов на ЭВМ с целью

корректировки схемы усилителя измеренными или ранее известными стандартными S-параметрами. Однако более корректны в этом случае расчеты с традиционными S-параметрами, полученными в результате пересчета из нестандартных. Традиционные S-параметры наиболее просты для измерения; если же они измерены с точностью, достаточной для проектирования устройства, то задачу можно считать решенной. Основное затруднение при использовании традиционных S-параметров заключается в том, что они не измеряются с достаточной степенью точности. Чаще всего это связано с отсутствием специальной аппаратуры, с рассогласованием оконечных нагрузок, наличием в измерительном тракте коаксиаль-но-полосковых переходов и прочих неоднородных эле-56

ментов. Поэтому разные системы параметров могут быть неравноценными и преимущество должно быть отдано той, которая гарантирует наибольшую точность расчета. Системы нестандартных параметров, включающие непосредственно данные, необходимые для проектирования усилителей, представляются хорошо согласованными с экспериментом и поэтому их целесообразно использовать.

Глава 3

УТОЧНЕНИЕ ФИЗИЧЕСКОЙ МОДЕЛИ СВЧ ТРАНЗИСТОРА И ЕЕ АНАЛИЗ

3.1. ВЫБОР МОДЕЛИ И ТАБУЛИРОВАНИЕ S-ПАРАМЕТРОВ

В данном параграфе решается несколько задач.

Первая из них заключается в том, чтобы выбрать подходящую по сложности физическую модель (эквивалентную схему) и найти соотношения, связывающие S-параметры, а следовательно, и все остальные характеристики транзистора с параметрами этой модели.

Вторая задача состоит в том, чтобы вычислить и про-табулировать эти S-параметры для широкого набора типовых значений выбранной модели. Во многих случаях, сравнивая измеренные частотные характеристики с табулированными, разработчик сможет выбрать удовлетворяющую его модель.

Если достигнутое соответствие неудовлетворительно, необходимо согласовать характеристики структурных (физических) моделей с более точными экспериментальными характеристиками бесструктурных моделей, т. е. так изменить параметры структурных моделей, чтобы их выходные электрические параметры (например, S-параметры) соответствовали экспериментальным. В этом заключается третья задача этого параграфа.

В гл. 1 была проанализирована простая модель (рис. 1.4) при сопротивлении нагрузки i?H=0. Поскольку эта модель недостаточно точно отражает поведение СВЧ транзисторов в общем случае, рассмотрим теперь более полную модель (рис. 1.13,6) при произвольных внутреннем сопротивлении генератора и нагрузке. (К сожалению, усложнение схемы и вынужденное применение мат-

ричных методов анализа цепей приводит к потере наглядности.)

Рассмотрим сначала СВЧ транзистор, представленный упомянутой моделью, при единичных стандартных (/?h=Rr=50 Ом) нагрузках (рис. 3.1,а).

Частотные характеристики, рассчитанные на ЭВМ с помощью этой модели, достаточно хорошо отражают поведение реальных транзисторов. К произвольным нагрузкам мы далее перейдем с помощью общих соотношений, иредставлеиных в § 2.4.

Связь низкочастотных параметров выбранной модели с внешними характеристиками усилителя выявим через параметры матрицы рассеяния. Это удобно методически, поскольку анализ СВЧ усилителей проводится нами в терминах этой матрицы. Кроме того, это позволяет без дополнительных расчетов сравнивать данные экспериментальных исследований СВЧ транзисторов с расчетными,

Методика измерения и Исследований стандартных S-параметров СВЧ транзисторов описана в [3.1].

Система уравнений для узловых напряжений модели на рис. 3.1 имеет вид

О

о

где

1 +]д

j/(/б) о

о

j/(/б) ь

О

О

е

(3.1)

I -ос

Гб кэ/(Ч-ЯСэ'-э)]т-р/э

[rsf(l+iQcr)\ + lQls

e=l-f jQ (с + Сз + с„).

В системе (3.1) нормированные безразмерные значения элементов схемы на рис. 3.1 и частоты связаны с истинными значениями этих параметров соотношениями:

Здесь соответственно истинные значения сопротивлений базы, эмиттера и внешних генераторов, индуктивностей базы и эмиттера и емкостей - активной, пассивной, коллекторного перехода и корпуса; строчными буквами обозначены соответствующие нормированные (ксо^ и Rt) параметры; со и -текущее значение частоты и критическая частота базы; a=au{cosmQ~lsinmQ)f +]й) (1+] ЙСэГэ)-коэффициент передачи тока теоретической модели СВЧ транзистора с учетом емкости эмиттерного перехода Сэ; m=m-j-K)a H7g/(2yj) (см. (1.31)). Решение системы уравнений (3.1) относительно Uj

Uj=IA,jI (3.2)

позволит связать S-параметры, характеризующие модель транзистора, с ее НЧ параметрами. При вычислении S-параметров воспользуемся их определениями, следующими из (2.21), а также вспомним, что 17=ипад+1/отр,

tiEi (поскольку Гг=/н=1), Vuan=Eil2. С уЧбТОМ ЭТИХ

замечаний

S., = 2, S = 2-l, (3.3)

где Д - определитель системы; Д^, - его алгебраические дополнения.

Результаты вычисления S-параметров для типовых параметров физической модели приведены в табл. 8 приложения 5. В табл. П.9 приложения 5 представлены результаты вычисления номинального коэффициента усиления при двустороннем согласовании Ghomi,2 Для рассматриваемой модели (см. подробнее [3.1]).Ее детальный анализ содержится в § 3.3.

Включение маломощных транзисторов по схеме с ОБ применяется на СВЧ значительно реже, чем с ОЭ. Это в значительной степени связано с недостаточной устойчивостью этой схемы. В отличие от схемы с ОЭ, имеющей широкую частотную область безусловной устойчивости, схема с ОБ потенциально неустойчива в большей части частотного диапазона. Соотношение К>\ нередко выполняется для этой схемы в области частот, где Сном1,2 транзистора столь мало, что практически он не может быть использован как усилитель. Более того, в большой области частот выходные сопротивления СВЧ транзистора отрицательны. Однако, несмотря на трудности, связанные с обеспечением устойчивости СВЧ транзисторов, включенных по схеме с ОБ, их потенциальные возможности на СВЧ далеко не исчерпаны; поэтому исследование их моделей представляет существенный интерес (подробнее см. § 3.2).

Матрица узловых напряжений для физической модели транзистора, включенного по схеме с ОБ (рис. 3.1,6) имеет тот же вид, что и (3.1): 1

О -

(3.4)

где а=1

= l+jfi(c, + c + 0-

/ Решение системы уравнений, определяемой матрицей (3.4), то же, что и для матрицы (3.1). Оно представлено в терминах S-параметров выражениями (3.3). Вычисленные на ЭВМ S-параметры, К и (У-функция для модели с типовыми для СВЧ транзисторов параметрами (теми же, что и для схемы с ОЭ), представлены в приложении 6. Эти результаты обсуждаются в § 3.2.

Модели на рис. 3.1 в основном удовлетворяют требованиям, вытекающим из решения прикладных задач в области анализа и синтеза транзисторных усилителей СВЧ. Более сложную физическую модель (рис. 3.2,а), отражающую большое число внешних паразитных элементов корпуса и структуры, целесообразно применять в исследовательских целях. В ней, в частности, учтены сопротивления контактов базы и толщи полупроводникового слоя за коллекторным переходом Гс. Она, в отличие от схемы на рис. 3.1,а, справедлива и в низкочастотной области, поскольку в ней отражено НЧ сопротивление коллекторного перехода /-oil/go- Анализ этой схемы полезен для определения влияния упомянутых элементов на передаточные и шумовые характеристики СВЧ транзисторов.

Для расчетов в НЧ области реактивные элементы модели можно не учитывать. НЧ модель, в которой Гбк и Дгэ объединены с Гб и Гэ, показана на рис. 3.2,6. Матрицы контурных токов и их решения для двух последних моделей представлены в приложениях 7 и 8.

При исследовании физической структуры СВЧ транзистора в процессе его разработки целесообразно учитывать неоднородность базового сопротивления в поперечном направлении, а также гребенчатую структуру прибора. Достоинством физической модели транзистора с одним эмиттером и двумя базами является то, что она отражает распределенный характер базового сопротив-

Рис. 3.2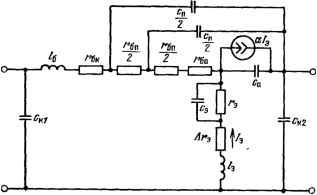

Рис. 3.3.

ления. Дополняя модель на рис. 1.12,в реактивными элементами корпуса получим физическую модель двухба-зового СВЧ транзистора (рис. 3.3).

3.2. МОДЕЛЬ С ОПТИМИЗИРОВАННЫМИ ЗНАЧЕНИЯМИ ПАРАМЕТРОВ

Выходные характеристики СВЧ транзисторов, полученные на основании физических моделей, лишь качественно соответствуют реальным характеристикам приборов. Типичная задача следующего этапа моделирования заключается в согласовании характеристик, вычисленных на основании моделей, с экспериментальными характеристиками. Это типичная оптимизационная зада-

т/е df/ffvemff S- переглгетроЮ

т

oHof/vcf e/F

Началбше

Анатв

Изменеть/е

Рис. 3.4

ча. Процесс моделирования рассматривается здесь как процесс нахождения таких значений элементов модели, при которых модель в наибольшей степени отражает поведение прибора. Общая схема оптимизации представлена в виде алгоритма на рис. 3.4. Процедура оптимизации, сводящаяся к сравнению расчетных значений параметров с экспериментальными с помощью выбранного критерия ошибки и последовательному уменьшению ошибки, описана в гл. 13.

0,5 Рис. 3 5

0,8 0,6 0. C.Z

7 0,1 0,3 0,4 0.5 0,6 0,7 0,8 Рис. 3.6

0,9 Q

На рис. 3.5, 3.6 построены частотные зависимости S-параметров для двух наборов параметров эквивалентной схемы на рис. 3.1,с. Значения одного набора приняты за эталонные (экспериментальные), второго - за начальные (последние показаны на рисунках штриховой линией). В процессе оптимизации начальные значения претерпевают существенные изменения, оптимизированные параметры эквивалентной схемы реализуют S-параметры, близкие к эталонным:

Сравнение характеристик прибора и модели в каждом конкретном случае показывает, каким образом достигается компромисс между точностью аппроксимации и сложностью модели. Если при оптимизации согласование характеристик достаточно, дальнейшее усложнение модели нецелесообразно. Чтобы ускорить процесс оптимизации на первом ее этапе нужно использовать относительно простые модели (рис. 3.1), усложняя их в дальнейшем введением дополнительных элементов, если первоначальные модели недостаточно полно описывают поведение реальных устройств.

Решение оптимизационной задачи в классическом виде требует сложных отработанных программ; иногда достаточна частичная оптимизация, т. е. согласование с экспериментальными лишь практически наиболее важных для синтеза параметров (Ghomi,2, К, Gmi)- Такую частичную оптимизацию иногда удается выполнить без специальных программ с помощью направленного перебора параметров эквивалентной схемы, осуществляемого на основании ее анализа (см. § 3.3).

Поскольку практические задачи синтеза в большинстве случаев удается решить по входным сопротивлениям транзистора в режиме двустороннего согласования (см. § 2.4) без привлечения эквивалентных схем, а при

5-384 §5