а коэффициент отражения описывается выражением (6.3) для I Гшах 12=0,5 (Гт1п| 2+1) И соответственно а2 =1, т. е.

I Р (Q) I = (х= + Q = )/( 1 + Q = ).

(6.26)

Общее решение задачи содержится в [6.20]. Здесь приведем соотношения для расчета элементов согласующей цепи при =3 (рис. 6.7,6). В этом случае

= gJsKV 2 g, - Y2 7ig, - 2), (6.27)

.g.+ xV.g. + 1) K2- (X- 1) + .-I-.f/l,

где

2 VT

A = Yl + l/r..

Зависимости значений элементов от сопротивления г. при п=3 и ==4 для двух значений gi показаны на рис. 6.8.

Рассмотренная реализация имеет еще одно интересное применение: нагрузка вместе с согласующей цепью образует низкочастотный фильтр (прототип) с потерями, сосредоточенными в индуктивных элементах. Актуальность таких фильтров связана, в частности, с возможностью их реализации в диапазоне CBI в виде микрополосковых интегральных схем с сосредоточенными индуктивными элементами, имеющими потери, существенно большие, чем емкостные элементы [6.28].

6.3. ШИРОКОПОЛОСНОЕ СОГЛАСОВАНИЕ

С ГЕНЕРАТОРОМ ДВУХЭЛЕМЕНТНЫХ КОМПЛЕКСНЫХ

НАГРУЗОК С ПОМОЩЬЮ ПОЛОСНО-ПРОПУСКАЮЩИХ

ЦЕПЕЙ

Постановка задачи и основные соотношения. В теории широкополосного согласования комплексных сопротивлений, развитой в работе Фано и его последователей [6.2, 6.6], обычно рассматривается согласование комплексной нагрузки с генератором, внутреннее сопротивление которого не оговаривается. Последующее преобразование входного сопротивления согласующего четырехполюсника, нагруженного на согласуемое сопротивление, к уровню внутреннего сопротивления генератора осуществляется в этом случае с помощью идеального трансформатора. Практические трудности реализации трансформаторов с характеристиками, близкими к идеальным, делают актуальным рассмотрение цепей, обеспечивающих нужный трансформирующий эффект непосредственно (без трансформаторов). Особую актуальность такие цепи приобретают в интегральных схемах ВЧ и СВЧ. где элементы с взаимными индуктивностями трудноосуществимы, а четвертьволновые распределенные трансформаторы чрезмерно громоздки. С другой стороны, успехи технологии позволяют создавать элементы цепей с линейными размерами, намного меньшими длины волны в нижней части сантиметрового диапазона (см., например, [6.29-6.31]), а следовательно, и цепи с сосредоточенными постоянными в СВЧ диапазоне. Таким согласующим цепям посвящена работа [6.13]; однако предельные соотношения представлены в ней лишь в графическом виде, а расчет параметров элементов цепи 10-384 145

Треисфврма1{ия вверх

I----1 1 о,2п-1 /?гл+; ----1

требует значительных усилий. В отличие от [6.13] элементы первоначальной полосно-пропускающей цепи определяются нами с помощью простых рекуррентных соотношений для прототипов этой цепи (см. § 6.2). Последние позволяют найти аналитическое решение задачи.

Синтез согласующей цепи сводится к нахождению соотношений между коэффициентом трансформации сопротивления К, полосой пропускания ш=Л(о/соо и максимально допустимым коэффициентом отражения на клеммах генератора Гтах, а также к определению эле- ментов согласующей цепи. Согласующие цепи, предна- значенные для согласования комплексных нагрузок различных типов, показаны на рис. 6.9. Схемы в левом столбце осуществляют трансформацию вниз, в правом - вверх. Нагрузки обведены на рисунке штриховой ли-нией. Варианты цепей на рис. 6.9 а-г берут начало от прототипов с четным числом реактивных элементов п, а на рис. 6.9,а'-е' - от нечетных. Рассматриваемые цепи содержат 2 реактивных элементов. Все элементы цепей LCR нормализованы относительно активной части

согласуемой нагрузки Rx и средней частоты полосы пропускания (оо. Индуктивные и емкостные элементы цепи составляют aii=(iioLilRu aic=tooCt7?i, сопротивление согласуемой нагрузки Г1=1, а генератора Г2 +1=/С. Можно показать (см. приложение И), что соотношения для определения элементов и коэффициента трансформации сопротивления согласующих цепей, изображенных на рис. 6.9,fl, б, имеют вид:

g2m-iS

т

8п

гп = -- при п - нечетном;

т

где

Л^т=1/(1+г= -,гЛ

(6.28)

/п= 1, 2

при четном п.

при нечетном п.

Соотношения, необходимые для вычисления элементов НЧ прототипов для чебышевского и максимально-плоского приближений при п=2 ... 4 приведены в приложении 9: вспомогательные величины х, у= =/(Гтах, п), необходимые для вычисления г, - в приложении 10.

Обращенные схемы на рис. 6.9,е, г характеризуются обратными значениями элементов. Так, например,

4; -p=JKm-r (6.29)

10* 147

Если требуется реализовать коэффициент трансформации /С' (/С'. ), отличный от расчетного j.= +,X

т

ХДЛ^т- параллельно элементам а. . в схемах на

рис. 6.9,а, в и последовательно им в схемах на

рис. 6.9,6, г включаются избыточные (по отношению к 2п) реактивные элементы

a-zg2rbNml (g2rn-lg2mbNm + Nm-\), (6.30)

знаки которых обратны а4т-з-

Значения Nm в (6.30) и (6.28) для вычисления всех остальных Ог должны быть определены в этом случае из соотношения

К' -! -г' ТТл^

(6.31)

в этом случае при вычислении щ в (6.28) Nm следует заменить на Nm- Очевидно, что избыточные элементы уменьшают трансформируюшие свойства согласующей цепи.

Для удобства приведем следующие из (6.28) соотношения, позволяющие находить элементы наиболее простых ( =2 ... 5) согласующих цепей (рис. 6.10).

Элементы цепей (рис. 6.10,а), трансформирующих вниз сопротивление согласуемой ]?С-нагрузки, равны

ai=gi6, a2=Nig26, a3=AV26/(l-Ai), ai=mg26№i), r=rN\ при = 2; ab=gzK аб==1/а5, ry=riN\ при n=3; a5=g3mb ae = NiN2g46, a7=N\mg,bl{\-N); a8=-1 / ig4bNiN2), rg=rjiNiN2 при n=4; aggsNiNmz), aio = l/a9, rn = rN\N\ при = 5,

(6.32)

где iV,=l/(l + g,262); iV2=l/(l+3g462); gi, r +,-элементы НЧ прототипов (см. приложение 9); gi с одина-наковыми индексами различны для разных и; формулы для oi ... 04, oi ... as одинаковы для разных п.

Значения реактивных элементов согласующей схемы для параллельной 7?1-нагрузки обратны по ртношению 148

Puc. 610

к значениям, определенным (6.32). Так, например, при =2 (рис. 6.10,е)

а,=1/(,б), a2=l/(iV.26),

a3=(l-iVi)/(iV2.g26), a4=g26iV2i. (6.33)

Наконец, значения реактивных элементов для простейшей схемы, согласующей нагрузку с последовательными реактивными элементами (рис. 6.10,(3), которыми

могут быть индуктивность, емкость или резонансный контур,составляют

а1 = 1/Яз6г'4, а2=Язбг4, 03=/26, 04=26/(l-iVi)r4, 05=26/ (JV,r4), a6=gi6/4iV2,. (6.34)

Общие формулы для расчета элементов согласующей цепи для последнего случая, а также для дуальной схемы на рис. 6.10,е' приведены в работе [6.15]. Рассмотренные схемы, изображенные на рис. 6.10,а, в, д\ трансформируют сопротивление согласуемой нагрузки вниз (т. е. уменьшают его), значения внутренних сопротивлений генераторов Г5, г?, ... этих схем определены соотношениями (6.28). Они в rzNu riNi, ... раз меньше сопротивления нагрузки ri=l.

На рис. 6.10,6, г, е' помещены схемы, дуальные по отношению к первоначальным. Они трансформируют сопротивление нагрузки вверх. Значения реактивных элементов этих схем вычисляются по тем же соотношениям, что и для первоначальных, а сопротивления генераторов обратны им (т. е. г5 = 1/г'зЛ21, r7=lfriNi и т. д.).

Сопротивление генератора (коэффициент трансформации сопротивления) можно представить как зависимость K-f{x, у, б) [6.15]. Так, для п=2

4 = +.=

(6.35)

Анализ результатов. Рассмотрим общие закономерности полученных соотношений. Прежде всего заметим, что трансформирующие свойства цепей (К^, i/K) уве-

личиваютсяс уменьшением w, увеличением Г^а^ и п

(рис. 6. 11). Для чебышевского приближения это влияние различно при четном и нечетном п. Нетрудно показать, что для четных п г„., не зависит от пи К увеличивается (а уменьшается) с уменьшением у из-за

уменьшения Nm, достигая минимального значения при у=0 и обеспечивая, таким образом, больший трансформирующий эффект, чем при рассмотренных в [6.13] оптимальных значениях х к у.

Как уже упоминалось, цепь при этом является оптимальной В том смысле, что при заданных ai и Гшах 150

имеет максимальную полосу пропускания или, что То же, минимальное значение а, при заданных б и Гтах и одном и том же п. Когда реактивный элемент ai согласуемой нагрузки препятствует достижению требуемой полосы пропускания, такая оптимальная реализация является действительно оптимальной. Если же это ограничение отсутствует, а требуется обеспечить максимальный трансформирующий эффект, то наиболее пригодно чебыщевское приближение при :/=0. Более того, при одном и том же К эта реализация обеспечивает более широкую полосу пропускания, чем реализация с оптимальными X \\ у, из-за меньших значений первого реактивного элемента щ.

Заметим далее, что кривые К для разных п и одинаковых Гтах имеют ОДНО И ТО жс начальнос значение при 6=0, поскольку при 6=0 все Л^ в (6.28) равны единице, а г„+1 является функцией только Гтах, но не п. Последнее объясняется тем, что бесконечно большая полоса (6=0) реализуется прототипом с бесконечно малыми реактивными элементами. Для чебышевского приближения при нечетном п кривые /С^ не достигают максимальных значений при y=Q и проходят в отличие от четных реализаций ниже оптимальных кривых. При у- =0 для нечетных п r +i = l, поэтому кривые К проходят через начало координат графика /(=/(6). В отличие от четных п здесь К увеличивается с увеличением у (из-за уменьшения r +i), поэтому при оптимальных х, у реализация для нечетных п обладает большим трансформирующим эффектом, чем при у-0. Согласующие цепи с нечетным п являются менее эффективными, чем с четным, поскольку два последних элемента при нечетном п не трансформируют сопротивление нагрузки.

Максимально-плоское приближение коэффициента отражения дает существенно меньший трансформирующий эффект и требует существенно больших значений а\, чем чебышевское. Все кривые K=f{b) при г/=0 проходят через начало координат. С увеличением начального рассогласования (f/0) кривые /С^ =/(б) как для четных, так и для нечетных п проходят выше аналогичных кривых для у=:0 из-за уменьшения r +i.

Синтез согласующих цепей. В заключение рассмотрим, каким образом с помощью полученных соотношений осуществляется синтез. Рассмотрим наиболее общий

случай, когда заданы К, Ртах , 6, oi И задача заключается в нахождении элементов цепи. Вначале надо проверить, совместимы ли заданные условия. Для этого (при п=оо) они должны удовлетворять неравенству

<-

(6.36)

Если соотношения между Гтах, 6 и oi заданы так, что условие (6.36) выполнено, цепь позволяет получить в принципе любое К- Чтобы убедиться в этом, рассмотрим поведение К при увеличении п. Легко видеть, что

4sin

2t - 1

- n/2, x<\

л sin

2t+ 1 2rt

x= -b sin

= 4, (6.37

при этом 1\тК=оо. На практике большие п реализуют редко и при выборе Г^\, Ь, п (при заданном а,)

обычно идут на компромисс. Сложность синтеза бестрансформаторной цепи заключается в том, что реали- \r ax\ зуемая цепь должна обладать не только заданной полосой пропускания, но и нужным коэффициентом трансформации. При приемлемой сложности цепи этим требованиям удается удов-летворять далеко не всегда. Выбор значений элементов согласующей цепи может быть облегчен с помощью графиков, приведенных на рис. 6.11, 6.12. На рис. 6.12 представлены результаты решения уравнения =ai/6=2sin {л/2п)/{х - у) для чебышевского приближения при оптимальных х, у в координатах Гтах, u\W (это та же зависимость, что и на рис. 6.5, но в других координатах).

Как видно из кривых на рис. 6.5, 6.12, с увеличением числа элементов согласующей цепи или с увеличением допуска на коэффициент отражения может быть реали-

?,5 a,w

Рис. 6 12

зована большая ширина полосы пропускания (меньшая б) или одна и та же полоса пропускания может быть реализована при большем значении первого реактивного элемента oi- Напомним, что истинные значения элементов согласуемых RC- или /?1-нагрузок и полосы пропускания связаны с нормированными соотношениями:

/?,С==а,/<Во; L ?=ai/(Oo, Д(о=йо/б. (6.38)

Рассмотренные нерезонансные согласующие цепи позволяют согласовывать комплексные нагрузки и тогда, когда сопротивление генератора также комплексно. При этом модель каждого сопротивления генератора должна соответствовать соединению с нагрузкой последнего реактивного элемента в схемах на рис. 6.10. Из (6.28) можно найти ограничения на значения реактивных элементов модели генератора. Пусть нагрузка и генератор характеризуются соответственно параллельной и последовательной комбинациями RC и их желательно согласовать без включения трансформаторов. Для этой цели используем нерезонансную реализацию при п=2. Для НЧ прототипа этой цепи

Решая эти уравнения относительно хну, имеем

Поскольку IKgiN), а К^=г',1, окончательно имеем

Теперь очевидно, что минимальное произведение aj( определяется из условия у = 0:

( Л, (6.41)

6.4. ШИРОКОПОЛОСНОЕ СОГЛАСОВАНИЕ

С ГЕНЕРАТОРОМ КОМПЛЕКСНЫХ НАГРУЗОК

С НЕСКОЛЬКИМИ РЕАКТИВНЫМИ ЭЛЕМЕНТАМИ

Теория широкополосного согласования без идеальных трансформаторов (см. § 6.3) позволяет согласовать комплексную двухэлементную нагрузку с заданным со-

противлением Генератора. Как мы видели, в случае 1п(1/Гтах)<(яб/ai) задача может быть решена при заданных значениях К, Гшах, щ. При согласовании устройств, имеющих более сложные физические модели, типична другая задача, в которой модель нагрузки содержит несколько реактивных элементов. Решение задачи возможно и в этом случае, однако при нескольких реактивных элементах невозможно осуществить заданный уровень, трансформации и требуется вводить в согласующую схему трансформаторы комплексного сопротивления.

-о

ю

1 фо5.

1 фа.

Рис 613

Модель с двумя и тремя реактивными элементами.

Рассмотрим базовую модель с тремя реактивными элементами, имеющую структуру НЧ фильтра на рис. 6.13,а; модель с двумя реактивными элементами (рис. 6.13,в) получается из этой модели при аз=0. Соотношения для согласования моделей, реактивные элементы которых включены в других последовательностях, следуют из соотношения для согласования низкочастотной модели на рис. 6.13.

Известный метод синтеза цепей для согласования комплексных нагрузок требует вычисления элементов низкочастотных прототипов с помощью рекуррентных формул (6.19). В этом случае НЧ прототип преобразуется в полосовой фильтр путем настройки каждого элемента прототипа в резонанс соответствующей реактивностью. Затем осуществляется переход от НЧ прототипа к полосно-пропускающей цепи.

Такой метод сийтеза полосовых характеристик можно распространить на нагрузки, содержащие два или три реактивных элемента. Типичным примером такой нагрузки может служить диод (рис. 6.13,а). Поскольку в диод нельзя ввести реактивный элемент, непосредственная настройка в резонанс каждого его реактивного элемента невозможна. Физически осуществимая цепь реализуется с помощью примыкающего к нагрузке фильтра, пропускающего высокие частоты [6.32] (рис. 6.13,6).

Приведем формулы, пригодные для непосредственного синтеза нерезонансных звеньев (точнее, звеньев, не имеющих резонансов в полосе пропускания) полосовых согласующих цепей, позволяющие миновать этап предварительного определения их прототипов [6.8].

Пусть задача заключается в синтезе цепи, обладающей максимально-плоской или чебышевской амплитудно-частотной характеристикой коэффициента отражения (усиления для активной цепи) и обеспечивающей в полосе пропускания w коэффициент отражения Гтах (усиления Gmin) при неравномерности усиления в этой полосе Р= I Гшах I / I Гт1п 2. Возможная реализация такой цепи ( =3) изображена на рис. 6.13,6. Эта схема содержит подключенное к нагрузке нерезонансное звено, а при >3 дополняется последовательными и параллельными резонансными звеньями. Элементы схемы нормированы относительно модуля нагрузки и средней частоты полосы пропускания ио и являются здесь, в отличие от ненормированных величин, безразмерными параметрами. Нормированная частота Q=(o/(uo, анеч=шоО^?1; ач=МоЬ,/?1.

Для рещения поставленной задачи синтезируем НЧ цепь, преобразуем ее в резонансную полосно-про-пускающую, а затем в физически осуществимую нерезонансную цепь [4.1]. Элементы нерезонансной непи для чебышевского (Z=l) и максимально-плоского (Z=0) приближений имеют в этом случае вид [6.8]

8 282

°-JrГ^ °=~х=+ /-х /+28+0,752

282

°2°~ (х;= -Ь / + ху + 28= + 0,75Z) (1 - <х,а,)

а

1 - а,Ог

1 - г з + 1 г°з 2 (1 - 1 г)

аз(1 - а2аз + а,а%(Хз)

(6.42)

Здесь Z=0 для максимально-плоского приближения, Z=l для чебышевского. Общие выражения для вычисления элементов цепи любой сложности, содержащие выражения для вычисления элементов резонансных звеньев, приведены в [4.1].

Заметим, что для получения оптимальной цепи, т. е. цепи, обладающей наибольшей полосой пропускания при заданном коэффициенте отражения (усиления) и числе элементов 2п, величины х и у должны быть предварительно оптимизированы по Фано [6.2].

Уравнения (6.42) позволяют синтезировать чебышев-скую полосно-пропускающую цепь при заданных значениях элементов нагрузки аь аг, аз и определить достижимые в этом случае значения полосы пропускания, коэффициента отражения (усиления) и неравномерности. Для этого три первые уравнения (6.42) должны быть решены относительно б, х, у. Практически более важна, однако, другая задача, когда заданы oi, аг и 6=1 [w, поскольку полоса пропускания w обычно является исходным параметром, а оз может быть дополнен до требуемого значения емкостью внешнего элемента. Решение в этом случае имеет вид

= а,(1-а,а,)

3in2 eos2--cosjZ

82 sin

3n 2n

5n 2n

5n 2n

Гшах2=(В2+1)/(2+1), = АЦ1+В^)1ВЦ1+А^1),

(6.43)

где

A = shmTcshx; В=sh n arcsh у; Z=l, (6.44)

для чебышевской характеристики; A==x, В=у', Z-0 для максимально-плоской. (В данном случае при заданных аь аг, аз решение также определяется выражениями (6.43) с той разницей, что первое уравнение (6.43) необходимо разрешить относительно б.)

Перед решением задачи полезно проверить, возможна ли реализация лестничной схемы при данных значениях б, 02 (эти вопросы также рассмотрены в работе [6.8]). Модель с двумя реактивными элементами на рис. 6.13,в можно трактовать как частный случай модели на рис. 6.13,а. Согласующие цепи вместе с моделями таких нагрузок изображены на рис. 6.13,6, г. Их элементы определяются соотношениями (6.42), (6.43) и соответственно (6.33).

Модели с тремя реактивными элементами, соединенными в различных сочетаниях, показаны на рис. 6.14. Рис. 6.14 Модель, изображенная на

рис. 6.14,а, дуальна основной модели (рис. 6.13,6). Две других модели (рис. 6.14,6, в) являются обращенными по отношению к первым двум (рис. 6.13,6, 6.14,а) и характеризуются обратными значениями элементов (ajo6p=l/од).

Таким образом, полученные соотношения позволяют выполнить строгий синтез некоторого класса согласующих широкополосных схем. При этом могут быть заданы три независимых параметра, например: Гтах (Сшш), Р, б, или щ, 2, или аь 02, аз.

В первом случае результатом синтеза являются требования к элементам нагрузки (например, транзистора) и значения элементов согласующей схемы (задание неравномерности р обычно имеет смысл при синтезе АЧХ с активными полупроводниковыми приборами, например при синтезе АЧХ туннельного усилителя). Во втором случае результатом синтеза является значение аз и согласующей схемы; при этом появляется некоторая свобода в выборе третьего реактивного элемента, который может быть дополнен до расчетного значения ссз внешним реактивным элементом того же знака.

В последнем случае все три элемента ai, az, Оз зада-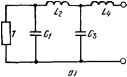

Рис. 6.15

ны и результатом является синтез согласующей схемы. Полоса пропускания Гтах и р в этой схеме определяются тремя заданными элементами нагрузки. Можно показать, что для согласования НЧ модели с четырьмя реактивными элементами (рис. 6.15,а) потребуется согласующая цепь со структурой ВЧ фильтра (рис. 6.15,6). Синтез такой цепи описан в [4.1].

6 5. СОГЛАСОВАНИЕ ДВУХЭЛЕМЕНТНЫХ КОМПЛЕКСНЫХ НАГРУЗОК С ПОМОЩЬЮ ПРОСТЕЙШИХ ЦЕПЕЙ С СОСРЕДОТОЧЕННЫМИ ПОСТОЯННЫМИ

Специфика проблемы широкополосного согласования в интегральных схемах СВЧ делает актуальным рассмотрение простейших согласующих цепей, имеющих минимальное число элементов. Несмотря на то, что такие цепи характеризуются значительно меньшей шириной полосы пропускания при тех же значениях первых реактивных элементов, чем цепи, рассмотренные в предыдущих параграфах, их широко применяют в интегральных микросхемах в силу их простоты.

Интерес к таким цепям находит отражение в ряде работ, появившихся в последнее время. В отличие от этих работ, рассмотрение в которых ограничено согласованием комплексной нагрузки с активным генератором [6.33-6.36] или в которых практически не рассматриваются частотные характеристики согласующих цепей [6.33, 6.35-6.37], здесь исследовано в диапазоне частот согласование произвольных двухэлементных комплексных нагрузок, а случай активного генератора является частным. (Произвольная комплексная нагрузка может быть представлена с помощью двух элементов: активного и реактивного - на фиксированной частоте точно, а в диапазоне частот с известным приближением.)

hrt) д,

(1-1*)

11 ( г Il г f{ г'/;

о о-*-0 0-*-о 0-*-оо-

-о о

-о

г 1 -о о

мэ CH-JI-o о

zi\ г 1\ г г л о о*-о о*-о о

В) 5е)

Рис. 616

Для точного согласования на одной фиксированной частоте двух комплексных нагрузок с составляющими R и X (рис. 6.16) необходима цепь, имеющая две степени свободы. В цепях с сосредоточенными постоянными это эквивалентно двум реактивным элементам. Различные комбинации комплексных нагрузок и согласующих цепей представлены на рис. 6.16 {1-8). Схемы на рис.6.16 (1а-8а) являются дуальными по отношению к первоначальным.

На этих рисунках нормированные к Rt значения элементов, равные относительным реактивным сопротивлениям (д:) и проводимостям (&), составляют r\=.RilRr, Г5=/?г ?г=1 для нагрузки и генератора, д:с=-1/мС7?г и bc=(i)CRT для емкости, xi=aLlRj. и bi=-RrlaL для индуктивности.

Элементы согласующих цепей найдем из условия равенства нулю коэффициента отражения на клеммах генератора (или нагрузки) на фиксированной частоте ©0. (Хотя это требование и не является всегда оптималь-

ным в отношении широкополосности, расчеты показывают, что при простейших согласующих цепях условие 1Г(юо)0 не приводит к существенному расширению полосы пропускания.)

Условие (Г((оо)=0 сводится к одновременному выполнению на клеммах генератора двух условий:

RezBx=l, 1тгвх=0 для схем 1-4,

Не/вх=1, 1т^/вх = 0 для схем 5-8. (6.45)

Решение уравнений (6.45) имеет вид

Х2 = тМ-Хи bz=(mM+Xiri)/((l + xi)ri) (6.46)

для схем /-4 Ь2=тН-Ьй

X3=(mH-\-bigi)l((l-b)g,) (6.47)

для схем 5-8,

где

Ж=[г.(1 +дг*,)-гМ ; H=.{g,(l + b\)-g\f ;

Анализ (6.46), (6.47) позволяет найти ограничения, накладываемые рассматриваемыми схемами на величины согласуемых элементов Гь Хх и Х4 (или &4 для схем на рис. 6.16, 5 -8). Полученные при этом результаты для схем на рис. 6.16 (/-5) приведены в табл. 6.1. Для схем /-4 нагрузки представлены последовательным соединением двух элементов ги х, и п, х^, для схем 5-5 последовательным соединением п, Xi и параллельным &4, Г5. Для отыскания нужных схем и значений элементов дуальных схем (рис- 6.16, 1а-8а) в табл. 6.1 и в формулах (6.46), (6.47) необходимо заменить г на g и л: на 6.

Как следует из таблицы, при согласовании комплексной нагрузки с генератором введение четвертого реактивного элемента х^ (или &4) расширяет область допустимых значений г-у и х согласуемых данной схемой. Другой важный вывод заключается в том, что при всех допустимых значениях Г], л:, и ,4(64) всегда существуют либо два типа сопасующих цепей, либо одна и та же цепь, но с двумя различными значениями элементов. Окончательный выбор схемы можно сделать, исходя U-384 161

ш>4

я я ч о

CS Е-

ю

л

CO CO

л

л

о

g St

либо из поведения согласующих цепей вдали от полосЫ согласования (влияющего, например, :а устойчивость транзисторного уси 1ителя), либо из условия удобства реализации, либо из условия получения наибольшей полосы пропускания.

При рассмотрении частотных свойств разделим схемы на два класса. К одному отнесем схемы, структуры которых при соответствующих значениях элементов приводят к щирокополоснымхарактеристикам. Это каскад-но включенные фильтр~ы высоких и низких частот (на рис. 6.16 схемы 6, 7 при ri>l и 6а, Та при ri<l). К другому классу отнесем схемы, не имеющие такой структуры. Коэффициент отражения последних возра-стает в первом приб лижедии линейно^ с„уд£лшшн ем--расстройки. Результаты расчета полосы пропускания (по уровню rinaxt=0,l нз крэю полосы) при различныж -сочётаниях Г1 и (при 4=0) приведены ~ в работе

I6.38T:

6.6. ШИРОКОПОЛОСНОЕ СОГЛАСОВАНИЕ КОМПЛЕКСНЫХ НАГРУЗОК С ПОМОЩЬЮ ЦЕПЕЙ С РАСПРЕДЕЛЕННЫМИ ПОСТОЯННЫМИ

Простейшие согласующие цепи с распределенными постоянными. Применение в интегральных микросхемах СВЧ подложек с относительно большими значениями диэлектрической постоянной делает целесообразным реализацию этих схем, и в частности согласование комплексных сопротивлений с помощью цепей с распределенными постоянными. Наиболее простое решение проблемы, совместимое с возможностями микроэлектроники, состоит в согласовании комплексных нагрузок с помощью каскадно соединенных отрезков однородных линий.

Рассмотрим случай взаимного согласования двух комплексных нагрузок, когда в качестве согласующей цепи используется отрезок однородной линии. Варианты схем для этого случая показаны на рис. 6.17. Схема согласования с помощью одного отрезка относится к простейшей: степеня.ми свободы здесь являются длина линии и ее характеристическое сопротивление.

Параметры согласующей цепи, как и в случае простейших схем с сосредоточенными элементами, можно определить из условий равенства нулю коэффициента

И* 163