его связь с соседними блоками может или совсем отсутствовать, или быть очень слабой. На рис. 4.2 эти границы обозначены двойными штрихпунктирными линиями. Связи по этим каналам можно вообще не учитывать или учитывать лишь как паразитные.

В дальнейшем будет показано, как в соответствии с методом декомпозиции решаются различные ключевые задачи для конкретных направляющих структур и синтезируются пассивные устройства СВЧ.

§ 4.4 Дифракция электромагнитных волн на скачке ширины проводника экранированной МПЛ

Рассмотрим неоднородность в виде скачкообразного уменьшения ширины проводника экранированной микрополосковой линии (ЭМПЛ) (рис. 4.3). При решении этой задачи воспользуемся методом частичных областей. В соответствии с этим методом

всю область решения задачи разобьем поперечной плоскостью гг=0, проходящей через скачок, на две частичные области, представляющие собой полубесконечные отрезки регулярных ЭМПЛ с шириной проводника Wi и W2 в соответствующих частичных областях. Будем считать при этом, что Wi< <wi. В предельном случае ширина полоскового проводника во второй области может быть равна нулю (г1У2=0 - обрыв проводника ЭМПЛ). Тогда вторая частичная область будет представлять собой двухслойный прямоугольный волновод.

Пусть плоская электромагнитная волна падает слева на неоднородность. В этом случае поле в первой области представляет суперпозицию полей падающей и отраженной от неоднородности волн. Во второй области имеется только прошедшая волна:

ы,1г о

Рис. 4.3. Скачок ширины полоскового проводника экранированной МПЛ

Е И

ei (A:, У)

ехр(-]р, г)+

Е Н

е, (А:, у) -Ь, (л:, у) j

е2 (А-, у)

. 2п^Х, У) J

ехр(1Р, г) при г<0, (4.6)

exp(-]M при 2>0, (4.7)

где I i 1 2-система собственных функций сече-

I hy {X, у) I

ния соответствующей регулярной линии; An, В„н С„ - неизвестные коэффициенты.

Граничные условия на стыке обеих областей в плоскости г=0 запишем в виде векторных произведений:

[Е„ Zol = [E2, Zol на S, (4.8)

[Zo. H,I = [zo, H2I на 5 (4.9)

[El, Zol = [E2, Zol на ASS-S, (4.10)

где Si и S2 - части сечений соответствующих регулярных линий, свободные от проводников; zo - единичный вектор, направленный вдоль оси Z.

Подставив (4.6) и (4.7) в (4.8), учитывая ортогональность собственных функций области 2 и условие (4.10), получим систему уравнений

л = 1

(4.11)

где

Л'2ft .1

A2ft=j kft, h2t]zofi?5, k=\, 2, 3, Аналогично, используя условие (4.9), получаем

(4.12)

где

-nk

Сщ, h2ft]zoCfs, \п, h* ]zofi?5.

Систему линейных алгебраических уравнений (СЛАУ) (4 11) и (4.12) можно переписать в виде: > \ i

d.nBibun-bntC

n-l п-1 \ i-i

(4.13)

Решая бесконечную СЛАУ (4.13), находим коэффициенты разложений (4.6) и (4.7), т. е. получаем выражения для поля отраженных и прошедших волн.

Аналогично, решая задачу при падении волны на неоднородность справа, получаем СЛАУ относительно коэффициентов разложений для отраженной и прошедшей волн:

п-1 л-1

N 1 ~ \

(4.14)

п-1 п-1 \ /=1 /

Коэффициенты СЛАУ (4.13) и (4.14) выражаются через дифракционные интегралы вида . Х„л= [е, , h*ik]Xzods, для вы-

числения которых необходимо знать собственные функции регулярных линий обеих областей. (Методика получения этих функций была рассмотрена в § 1.1.) Они определяют два класса волн, которые могут существовать в этих линиях: LE(EysO) и

Матрица рассеяния получается в результате решения СЛАУ (4.13) и (4.14). Для вычисления /-го столбца указанной матрицы следует решить СЛАУ при условии, что в ее правой части А,= 1, Ai=0 (/=7/). Полученные коэффициенты разложений и

{Сп} являются элементами матрицы рассеяния.

§ 4.5. Дифракция электромагнитных волн на двух близко расположенных скачках ширины полоскового проводника МПЛ

По рассмотренному в предыдущем параграфе алгоритму можно получать матрицы рассеяния и более сложных неоднородностей. Но если две неоднородности расположены на небольшом расстоянии друг от друга, то запредельные высшие типы волн, возникающие на каждой из них, не успевают затухнуть на малом участке линии между этими неоднородностями. В результате возникает очень сложная картина поля, для описания которой матрицы рассеяния каждой неоднородности должны иметь очень высокий порядок, что требует большой оперативной намяло

I 3

Е

ти ЭВМ и приводит к чрезмерному расходу машинного времени. Поэтому для исследования таких неоднородностей необходим специальный алгоритм.

Получим этот алгоритм. Типичная структура неоднородности в виде двойного скачка ширины проводника МПЛ представлена на рис. 4.4. Соотношения между шириной полосковых проводников могут быть различными, порядок следования скачков тоже может быть произвольным (сужение - расширение - см. рис. 4.4, расширение - сужение, расширение - расширение, сужение - сужение). В отдельных областях ширина полоскового проводника может быть равной нулю.

Электромагнитное поле в областях У и 2 представим в виде суперпозиции падающих и отраженных волн, а в области 3 - в виде суперпозиции только прошедших волн. Поля в области 1 запишем в виде

е

Рис. 4.4. Неоднородность в виде двойного скачка ширины полоскового проводника экранированной МПЛ

Е Н

= 2 Л

ехр(-]р, г) +

+ 25п

в области 2

-Ьхл

exp(jP, 2);

(4.15)

Е Н

11 i - t2n

ехр(-]р2лг) + ехр(]Р2л2);

в области 3

Е Н

3 п-1

ехр1-]рз (г-г,)].

(4.16)

(4.17)

где

1 Суп

-системы собственных функций поперечного сечения

области /; В„, Сп, Dn, Fn - неизвестные коэффициенты.

Для структуры, приведенной на рис. 4.4, граничные условия на границах между областями запишем в виде:

[Е,. Zo] = IE2, Zp] на 2 при zO, (4.18)

[Е,. Zo] = [E2. z,]=0 на А8о=3,-8г при z=0, (4.19)

[Zp. H,] = [Zo, Нг] на 5, при z=0, (4.20)

[Eg, Zol = [E2, Zpl на 2 при z = Zi, (4.21)

[Ез, ZoI=:[E2, Zo] = 0 на ASS-Ss при 2=г„ (4.22)

[Zp, H3] = Izo, H2] на S3 при z=z (4.23)

где Sj - поперечное сечение полосковой линии в области /. В случае бесконечно тонких полосковых проводников поперечные сечения вырождаются в отрезки.

Подставив в равенства (4.18) - (4.23) выражения (4.15) - (4.17) и воспользовавшись ортогональностью собственных волн в каждой области

f [су, h*fk]zods=0 при пфк.

получим бесконечную СЛАУ относительно коэффициентов Вп, Сп, Dn и Fn- Исключив из нее коэффициенты С„ и Dn, получим систему уравнений относительно Вп и F :

2 2 nin-nn);

л-1 п=1

o.nnFn-V\% пВп^АХип,

п-1 п-1 л-1

где k=\, 2, 3,...;

Ckpfnp

] sin {2pZl)

*л = 8йл + У -р-1

оо /7-1

iig(hpzi) hpfnp

]tg(P2p2i)

] sin (рзр^О

fittp=-~- f [cin. h2plzorfs;

]zoCf5;

p--a7 np ftp-

bnp.

*g]zQds, j=l, 2, 3.

Здесь g==g=-1 - параметры, определяемые структурой неоднородностей. Указанные параметры могут принимать значения ± 1 в различных сочетаниях.

Таким образом, получена математическая модель для двойного скачка ширины проводника при S2Si, S3 (см. рис. 4.4).

Для структуры, в которой S2Si, S3, необходимо в граничных условиях (4.18) - (4.20) произвести замену Si- ->-S2, а в условиях (4.21)-4.23)-замену S2- -S3; при этом g=g=l. Для структуры, в которой SiS2S3, производят замену S2- ->-S3 в условиях (4.21) - (4.23), а параметры I и I принимают значения - 1 и -Ь1 соответственно. Наконец, для получения математической модели структуры, у которой SiSaSa, необходимо выполнить замену Si-<- -S2 в условиях (4.18)-(4.20), а параметрам g и присвоить значения -f-l и -1 соответственно.

§ 4.6. Нерегулярный полосковый тракт с каскадно включенными неоднородностями

Тракт СВЧ на линиях передачи любого типа всегда можно представить в виде совокупности каскадно включенных базовых элементов трех типов: отрезков регулярных линий передачи, отдельных неоднородностей линий передачи и двойных неоднородностей. Поэтому анализ нерегулярного тракта СВЧ можно проводить методом декомпозиции.

В виде отдельных неоднородностей базовые элементы используются в том случае, когда неоднородность располагается между отрезками регулярных линий достаточно большой длины и можно считать, что только конечное число волн высших типов, возникающих на этой неоднородности, будет взаимодействовать с соседними неоднородностями слева и справа. В виде двойной неоднородности элемент рассматривается в том случае, когда эти неоднородности расположены настолько близко друг к другу, что ограничиться сравнительно небольшим числом волн высших типов, возникающих на каждой из этих неоднородностей, нельзя.

Рассмотрим полосковый нерегулярный тракт с каскадно включенными неоднородностями в виде скачков ширины полос-

KoBoro проводника. На рис. 4.5 показано его деление на отдельные блоки. Блоки /, 3. 5, 7. 9, 11. 13, 15 представляют отрезки регулярных полосковых линий, блоки 2, 6. 12. 14 - скачки ширины полоскового проводника, а блоки 4. 8, /-спаренные скач-

t 2 д 4 5 b 7 8 9 10 11 12 13 Н 15

Рис. 4.5. Полосковый тракт СВЧ с каскадно включенными неоднородностями

ки ширины полоскового проводника, расположенные на малых расстояниях друг от друга. Используя математические модели таких базовых элементов (см. § 4.3, 4.4), можно построить алгоритм вычисления элементов

/.

Рис. 4.6. Схема объединения многополюсников, описывающих базовые элементы неоднородной полосковой линии

матрицы рассеяния каждого базового элемента. Для этого каждый элемент представляют в виде многомодового четырехполюсника (рис. 4.6). Матрица рассеяния pS такого четырехполюсника состоит из четырех блоков и имеет порядок m+k, где т - число типов волн во входном его канале, п - число типов волн в выходном канале, р - порядковый номер четырехполюсника. Каждый блок представляет собой прямоугольную матрицу определенных размеров:

pS-mxm; pS-mx/t; pS--nxm; S-n хп. (4.24)

Если матрица pS одного из блоков рассматриваемого тракта имеет порядок m-frn, а матрица p+iS следующего блока - порядок n+k, то результирующая матрица p,p+iS имеет порядок т+ -\-k, элементы ее блоков можно вычислить по формулам (4.5), а размеры этих блоков определятся выражениями (4.24).

Результирующую матрицу рассеяния всего тракта можно получить по рассмотренной ранее рекуррентной схеме (см. § 4.2). По этой схеме на каждом шаге вычисляется матрица рассеяния соединения двух многополюсников - многополюсника, полученного на предыдущем этапе, и очередного базового элемента. Такая схема наиболее удобна для алгоритмизации.

А-А

§ 4.7. Дифракция электромагнитных волн на стыке двух многопроводных МПЛ

Рассмотрим стык двух различных МПЛ, показанных на рис. 4.7. Обозначим Si и Sz - части поперечных сечений соответствующих линий, свободные от проводников. Будем считать, что сечение проводников линии 2 целиком содержится в сечении проводников линии / (или, Sj содержится в S,). При решении задачи используем собственные волны многопроводных МПЛ, полученные в § 1.4.

Электромагнитное поле в линиях 1 Vi2 представим в виде суперпозиции падающих и рассеянных собственных волн соответствующих линий:

YZZZZZZZZZZZZZ.

Рис. 4.7. Стык многопроводиых МПЛ. Сечение проводников линии 2 целиком содержится в сечении проводников линии ;

/Е\ HJ

=2 ff Vp(-P >+i

(h) =2* ()exp(-JM+VZ),

\ /2 *ri \n2ft, jTl

ехр(]р1 г), (4.25)

exp(Jp2ft2).(4.26)

где

- системы собственных функций в соответствующих

линиях; An и - заданные амплитуды падающих волн; В„ и Cft - неизвестные амплитуды рассеянных волн; Л' и К-число типов падающих волн в соответствующих линиях.

Граничные условия на стыке линий (г=0), которым должны удовлетворять поля (4.25) и (4.26), запишутся в следующем виде:

[Е„ Zo] = [E2, Zp] на 5

[Hi, Zo]=jH2, Zp] на Su

[Ej, Zo1=0 на AS=S2-Si. (4.27)

Подставляя (4.25) и (4.26) в условия (4.27) и используя усло-

ВИЯ ортогональности собственных функций соответствующих линий и их нормировку в виде

[1, n = k.

получаем бесконечную СЛАУ относительно неизвестных амплитуд Вп и Cft рассеянных волн:

/ ~ \ Л' /

п-1 \ft-l / л-1

+2 2 1

2 1/* )~

*-1 у

(4.28)

е1л. h2*]zorf5, /, у=1, 2, 3....

Для получения численных результатов учитывают конечное число собственных волн в каждой линии, благодаря чему система (4.28) приобретает конечный порядок. Результат решения целесообразно представить в виде матрицы рассеяния. Чтобы получить матрицу рассеяния порядка п, необходимо при решении задачи рассмотреть п линейно независимых комбинаций падающих волн. Обычно задают последовательно по одной падающей волне единичной амплитуды. Тогда решение системы (4.27) определяет соответствующий столбец матрицы рассеяния.

В общем случае поперечные сечения проводников перекрываются лишь частично, т. е. ступеньки в ширине полосковых проводников существуют со стороны обеих линий. Непосредственное применение рассмотренного алгоритма к таким стыкам многопроводных МПЛ затруднительно, так как сложно учесть граничное условие £,==0 на проводниках в плоскости стыка со стороны обеих линий.

Чтобы упростить решение задачи, вводят в рассмотрение отрезок промежуточной линии нулевой длины, суммарное сечение

Рис. 4.8. Стык проводников МПЛ (общий случай)

проводников которой образовано множеством точек, являющихся пересечением или суммой множеств точек поперечных сечений проводников обеих исходных линий. Например, для стыка, представленного на рис. 4.8, промежуточная линия имеет ширину полоскового проводника, равную W\-b или W2-\-b.

Расчет матриц рассеяния стыков между исходными линиями и промежуточной выполняется по рассмотренному алгоритму, а расчет результирующей матрицы стыка - по формулам (4.5) для каскадного соединения многополюсников с известными матрицами рассеяния.

§ 4.8. Примеры реализации алгоритмов анализа ступенчатых неоднородностей МПЛ

Практическая ценность любого алгоритма определяется его характеристиками: скоростью сходимости, временем расчета, достигаемой точностью, устойчивостью, требуемой емкостью памяти ЭВМ. Эти характеристики зависят, в первую очередь, от вида используемых собственных функций регулярных участков волноводов. Алгоритм получения собственных функций регулярной ЭМПЛ с бесконечно тонким полосковым проводником с учетом особенностей поведения поля на ребрах проводника рассмотрен в § 1.1. Приведем результаты решения некоторых задач анализа различных ступенчатых неоднородностей ЭМПЛ.

Обрыв центрального проводника ЭМПЛ. При обрыве центрального проводника ЭМПЛ переходит в двухслойный прямоугольный волновод. Дисперсионные уравнения такого волновода *s/m2tga2+*s/2Hitgai=0, *s,ie2tgai-i-*s,2eitga2=0, где ei, jii и 82, Ц2 - диэлектрическая и магнитная проницаемость материала подложки и среды над подложкой соответственно, дают два упорядоченных массива поперечных волновых чисел kyin, соответствующих LM- и LE-волнам в двухслойном волноводе. Тогда последовательность постоянных распространения определяется из соотношения pmn==*oeij,i-(тп/ау-kyxn. Здесь а -размер широкой стенки экрана МПЛ; п - номер корня дисперсионного уравнения.

Для вычисления определенного числа членов этой последовательности, необходимого для достижения заданной точности вычислений, построен специальный алгоритм. Результаты расчета получены в виде матрицы рассеяния исследуемой неоднородности порядка 20X20, элементы которой при mlO соответствуют волнам ЭМПЛ, а при т>10 - волнам двухслойного волновода. На рис. 4.9 приведены зависимости модуля и фазы коэффициента отражения квази-Т-волны (Si,i) и коэффициента прохождения ее в двухслойный волновод (Si.n) от параметра оД. При переходе квази-Т-волны в двухслойный волновод происходит ее трансформация сначала в первую волну (ЬМю), а с

повышением частоты - и в последующие типы волн двухслойного волновода.

Как видно из приведенных графиков, на частотах, меньших критической частоты первой волны (ЬМю) двухслойного волновода (аД 0,41), модуль коэффициента отражения равен

единице. Двухслойный

0,6 0,6

G 0.1 0.2 ЦЗ W Q5 ио

-г

-ж

волновод является запредельным для всех типов волн. Поэтому они в нем не распространяются. На частотах выше критической частоты волны LMio модуль коэффициента отражения начинает монотонно убывать, а коэффициент прохождения растет, т. е. в двухслойном волноводе возникает волна LMio. На критической частоте второй волны двухслойного волновода (а/Х 0,66) на обеих кривых появляется излом, соответствующий появлению в двухслойном волноводе второй распространяющейся волны. Штриховая кривая соответствует нераспространяю-щейся (реактивно затухающей) волне в двухслойном волноводе.

Анализ полученных результатов показывает, что используемый алгоритм имеет достаточно быструю сходимость: уже в пятом приближении ошибка не превышала 1% даже на высоких частотах.

Скачок ширины проводника ЭМПЛ. Анализ скачка ширины центрального проводника ЭМПЛ проводился с помощью СЛАУ (4.13) и (4.14). Как и в случае обрыва проводника, была составлена матрица рассеяния исследуемой неоднородности порядка 20X20 с аналогичной нумерацией ее элементов. При исследовании предполагалось, что в направлении движения падающей волны происходит сужение проводника.

Исследования показали высокую точность определения элементов матрицы рассеяния и быструю сходимость алгоритма. Так, добавление пятого типа волны уже практически не изменя-

Рис. 4.9. Частотные зависимости элементов Si.i и Si,II матрицы рассеяния обрыва полоскового протодника

5f

<5>

о

Ч

оз о

о

я Э оо.

а

Я сз си

о а= т а

а о

S а

о S

£ §

ет фазы коэффициента отражения 5i,i, а ее модуль изменяется не более чем на 0,05% на самых высоких частотах. На рис. 4.10 приведены частотные зависимости коэффициента отражения и коэффициента прохождения волны основного типа на неоднородности в виде скачка ширины проводника для различных значений Wilwx. На кривых коэффициентов отражения на частоте возникновения волны первого высшего типа имеются скачки (см. кривые arg Si,i (аД)).

На рис. 4.11 представлена частотная зависимость действительной части коэффициента преобразования квази-Т-волны в прошедшую и отраженную волны первого высшего типа. Мнимая часть этих коэффициентов на несколько порядков меньше действительной, потому ее частотная зависимость не приводится.

Резонаторы и фильтры на связанных МПЛ. Микрополос-ковый резонатор, топология которого приведена на рис. 4.12,

0,Ь 0.5 OA 0.3 0,2 0,1 О 0,1 0.2 0.S OA

OA ReS,.

Рис. 4.11. Частотные зависимости действительной части коэффициента преобразования квази-Т-волны в прошедшую (S ,2) и отраженную (S1.2) волиы первого высшего типа на скачке ширины МПЛ

Рис. 4.12. Амплитудно-частотные характеристики резонатора иа связанных линиях:

St\ - коэффициент прохождения квази-Т-волны; Ssi - коэффициент преобразования волиы квази-Т в волну квази-LMio; h--0,05 а; Я-0,5с; /-0,3 а; ei-0,012a; 6s--0,052 а: №-0,048 с;-- - б,; -Oi

содержит три стыка между регулярными МПЛ. Проводники в среднем из этих стыков перекрываются лишь частично. Поэтому для его анализа необходимо ввести промежуточную линию нулевой длины (см. § 4.6). При анализе резонатора в соответствии с приведенными алгоритмами последовательно рассчитывались собственные волны регулярных МПЛ, дифракция на их стыках и матрица рассеяния всего резонатора.

На рис. 4.12 приведены также частотные зависимости некоторых элементов многомодовой матрицы рассеяния резонатора при двух разных значениях зазора б между полосковыми проводниками (при сильной и слабой связи между ними). В каждом отрезке линии учитывались основные волны (одна в несвязанных линиях и две - в связанных) и по два высших типа. Первой волной высшего типа была волна, близкая продольно-магнитной волне в двухслойном волноводе, получающемся после удаления из него полосковых проводников (квази-LMio); в рассматриваемом частотном диапазоне это распространяющаяся квази-Т-вол-на. Вторая высшая волна - реактивно затухающая (нераспро-страняющаяся).

Частотные зависимости элементов матрицы рассеяния (см. рис. 4.12) показывают, что при слабой связи в резонаторе кривые имеют более резко выраженный экстремум на резонансной частоте. Это означает, что при слабой связи значительно большая часть энергии волны типа квази-Т передается волне типа квази-LMio, чем при сильной связи.

Рассмотрим в качестве примера еще две микрополосковые структуры (рис. 4.13), которые могут быть использованы в устройствах СВЧ, в качестве развязок по постоянному току. Для их анализа удобно использовать приведенные алгоритмы. При расчете каждая структура разбивалась на каскадно включенные

Рис. 4.13. Разновидности микрополосковых развязывающих структур (а, б) и их амплитудно-частотные характеристики (в)

отрезки регулярных МПЛ: одиночных, двух- и трехпроводных. Стыки различных линий характеризуются матрицами рассеяния собственных волн линий передачи.

На рис. 4.13, в приведены амплитудно-частотные характеристики таких структур: резонатора с двусторонней связью (рис. 4.13, а) и звена из трех связанных МПЛ (рис. 4.13, б). Эти характеристики рассчитаны с учетом лишь основных (квази-Т)

волн (число таких волн равно числу полосковых проводников в линии). Как видим, структура на рис. 4.13, б обладает резонансными свойствами, которые усиливаются при увеличении ширины зазора б (при ослаблении связи между подводящими линиями и резонатором). Характеристики же звена, изображенного на рис. 4.13, а, являются очень пологими в достаточно большом диапазоне изменения величины б. Подобные звенья позволяют получить сильную связь между линиями при технологически допустимых зазорах и могут быть использованы, например, для развязки по постоянному току в схемах с активными элементами.

Анализ направленных ответвителей на связанных МПЛ. Расчет направленных ответвителей (НО) выполнялся в одномодо-вом приближении (без учета волн высших типов). Это обусловлено тем, что переход от подводящих линий к связанным выполняется не только в виде изменения ширины полоскового проводника, но и в виде поворота его на некоторый угол, что, в свою очередь, приводит к большим трудностям в разработке строгого

алгоритма расчета дифракции на таких неоднородностях. Поэтому при расчете НО поворотом полоскового проводника пренебрегаем. Представим НО как стык связанных и несвязанных МПЛ. При таком представлении НО можно использовать алгоритм решения задачи дифракции на стыках линий. Электромагнитные поля со стороны подводящих линий представляем в виде суперпозиции собственных волн несвязанных одиночных МПЛ. Ширина полосковых проводников в области связи и в подводящих линиях различна, поэтому в местах их стыков необходимо ввести промежуточные линии нулевой длины. Рассматривались два варианта промежуточных линий: несвязанные с шириной проводников как в области связи и связанные с шириной проводников как в подводящих линиях. Расчеты с обеими вариантами дали практически одинаковые результаты.

Амплитудно-частотные характеристики НО на трех связанных МПЛ приведены на рис. 4.14. Штриховыми линиями и точками показаны соответственно результаты расчета в квазиста-

ОЛ 0.5 0.6 0.7 О.В 0.9 1.0 (h/)-10

Рис. 4.14. Амплитудно-частотные характеристики трехпроводного НО на связанных линиях

тическом приближении и экспериментальные данные, сплошными линиями - результаты строгого расчета по описанным выше алгоритмам для стыка МПЛ. Сравнение с экспериментом подтверждает более высокую точность этих алгоритмов строгого расчета по сравнению с квазистатическими методами.

Синтез направленных ответвителей на связанных МПЛ. Задача синтеза НО на связанных МПЛ ставится следующим образом. Заданы параметры МПЛ, центральная частота и требуемая связь. Необходимо рассчитать все размеры НО таким образом, чтобы при согласовании с подводящими линиями обеспечивалась требуемая связь.

Заданная связь С12 представляет собой элемент S21 матрицы рассеяния, который зависит от зазора между проводниками в области связи б, длины области связи / и частоты ].

Аргументы функции 21 должны удовлетворять дополнительному условию, а именно: они должны быть определены таким образом, чтобы коэффициент отражения Su от области связи в подводящих линиях был минимальным:

min[S (8, та, /, /). (4.29)

Таким образом, задача сводится к решению трансцендентного уравнения

S2i(8, та, /, /) = С,2

(4.30)

при выполнении условия (4.29). Функции S21 и Sn вычисляются в соответствии с приведенными алгоритмами анализа НО. В уравнении (4.30) длина области связи / принимается равной полусумме четвертей длин волн четного и нечетного типов в области связи: /= (Хе+Хо)/8; переменной \ придаем значение, равное центральной частоте требуемого диапазона; при фиксированном зазоре б значение w вычисляется из условия (4.29). Связь S21 при этом считается функцией б. Если НО конструируется на связанных МПЛ различной ширины (w\ и Шг), то минимум Su отыскивается как минимум функции двух переменных

Wx и Wi.

ЧАСТЬ II

АКТИВНЫЕ МИКРОЭЛЕКТРОННЫЕ УСТРОЙСТВА СВЧ

ГЛАВА 5

ФИЗИЧЕСКИЕ ОСНОВЫ РАБОТЫ ГЕНЕРАТОРОВ СВЧ НА ДИОДАХ ГАННА

§ 5.1. Диод Ганна

Диод Ганна (ДГ) - это кристалл арсенида галлия электронной электропроводности с двумя омическими контактами на противоположных гранях (рис. 5.1). Активная часть ДГ обычно имеет длину Z=1...100 мкм и концентрацию легирующих донор-ных примесей /7о=2-10 *...2-10 см- Слои полупроводника с повышенной концентрацией примесей п' = = 10..10s см-з служат для создания омических контактов. Типичные значения диаметра кристалла d=50...250 мкм. Как видим, ДГ - это полупроводниковый прибор с двумя электродами, не содержащий р-п-переходов.

Название диодов связано с физическим эффектом, открытым Дж. Ганном в 1963 г. Эффект состоит в том, что при подаче на диод со структурой, показанной на рис. 5.1) постоянного напряжения, превышающего некоторый пороговый уровень Ыпор, возникают периодические колебания тока. Частота этих пролетных колебаний обратно пропорциональна длине активной части диода I:

Рис. 5.1. Структура диода Ганна

Лр=100 ,

(5.1)

где / - в мкм; /пр -в ГГц.

Таким образом, в отличие от многих типов автогенераторов, где колебания создаются в резонаторе, генераторы на ДГ в принципе могут работать без резонансных колебательных систем, i

По аналогии с диодами других типов электроды ДГ называют катодом и анодом, причем к катоду присоединяют отрицательный полюс источника постоянного напряжения, к аноду - положительный.

Параметры диода Ганна:

концентрация примесей в активной области По, подвижность электронов р,п в слабом электрическом поле (т. е. при напряжениях на диоде, меньших порогового);

длина активной области /, площадь контакта Л=л;й^/4;

пороговое напряжение Ыпор, пороговый ток /пор, сопротивление в слабом поле Ро=Ипор/пор, статическая емкость диода Со=еА/1.

Электрические параметры ДГ Ыпор, inop, Ro определяются по статической вольт-амперной характеристике (рис. 5.2).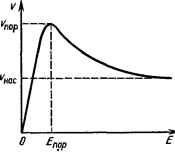

Рис. 5.2. Статическая вольт-амперная характеристика ДГ

Рис. 5.3. Зависимость средней дрейфовой скорости электронов от напряженности электрического поля в ар-сениде галлия н фосфиде индия

Краткие сведения о механизме работы диода Ганна. В основе эффекта Ганна лежит так называемый междолинный электронный переход. Для арсенида галлия (GaAs), фосфида индия (InP) и других полупроводниковых материалов характерна зависимость средней дрейфовой скорости электронов от напряженности приложенного электрического поля, изображенная на рис. 5.3. Особенность этой зависимости - наличие участка отрицательной крутизны.

Электрический ток в полупроводнике ia пропорционален скорости электронов v.

ignvA, (5.2)

где 0 - заряд электрона; п - концентрация электронов в активной области диода. Напряжение на электродах ДГ пропорционально напряженности электрического поля Е: Ua=El. Можно было бы ожидать, что статическая вольт-амперная характеристика ДГ повторяет зависимость v{E). Однако на практике этого не наблюдается, что можно объяснить неустойчивостью распределения электрического поля (£) в ДГ при Ыа>Ипор. Чтобы изучить картину распределения поля вдоль длины активной области диода, достаточно промоделировать процессы в диоде на ЭВМ.

§ 5.2. Математическая модель диода Ганна

Физические процессы в диоде Ганна могут быть изучены путем решения двух фундаментальных уравнений: уравнения Пуассона

cllvE=p/e . (5.3)

где р - плотность объемного заряда; во - диэлектрическая проницаемость полупроводникового материала (8а=еео, 8= = 12,5 для арсенида галлия), и уравнения плотности полного тока

divb=0. (5.4)

где

b=Jnp+W+JcM, (5.5)

- плотность полного тока; jnp - плотность тока проводимости; jдиФ - плотность диффузионного тока; Jcm - плотность тока смещения.

Следует отметить, что в структуре сэндвич (см. рис. 5.1) заряды движутся в одном направлении -от катода к аноду, поэтому можно полагать, что в плоскости поперечного сечения не изменяются ни плотность тока, ни электрическое поле. При таких допущениях задача упрощается и уравнения становятся одномерными.

Объемная плотность заряда

р=д^(п - По), (5.6)

где п - концентрация электронов; По - концентрация доноров. Плотность тока проводимости определяется выражением (5.2), плотность диффузионного тока в одномерном случае

U=-o-j. (5.7)

где D - коэффициент диффузии (в общем случае D=D{E), однако учет зависимости Ь от £ не приводит к новым результатам, поэтому для упрощения решения уравнений здесь принято D= =const);

Jc.=e,- (5.8)

- плотность тока смещения; t - время.

Уравнение (5.4) для одномерного случая имеет вид dji/(5x=0. Отсюда вытекает, что плотность суммарного тока внутри диода ji не зависит от координаты и может быть приравнена плотности тока и/А. протекающего через выводы диода во внешней цепи.

С учетом соотношений (5.2), (5.5)-(5.8) запишем уравнения (5.3), (5.4) в одномерном приближении:

дх ta

(5.9)

(5.10)

где ia - ток внешней цепи.

В уравнения (5.9) и (5.10) входят две неизвестные функции: п{х, t) и Е(х, t). Для удобства решения целесообразно (5.9) и (5J0) объединить в одно уравнение. С этой целью п из (5.9) подставим в (5.10), в результате получим

д^Е

дх dt djtr

-n,v(E)+

= 0.

(5.11)

При выводе уравнения (5.11) принято во внимание, что концентрация доноров По может изменяться вдоль координаты х, т. е. по==По{х). Нелинейные свойства диода учитываются тем, что скорость V зависит от Е.

Уравнение (5.11) будем решать в области О^х^/ при изменении времени / от О до оо. В этом случае для однозначного решения необходимо задать начальные и граничные условия.

В качестве начального условия нужно задать функцию Е{х) в начальный момент времени /=0. В качестве граничных условий необходимо задать функцию E(t) либо dE(t)/dt на границах активной области диода, т. е. при х=0 и х=1.

Начальное условие. Полагаем, что в начальный момент времени приложенное к диоду напряжение Ыа=0. При этом Е(х) = =0 в случае, когда dno/dx=0. Если же имеется градиент концентрации примесей, то возникает ток диффузии, образуются внутренние области зарядов и, как следствие, появляется ток проводимости.

В состоянии равновесия при Ыа=0 сумма токов проводимости и диффузионного должна быть равна нулю. Учитывая, что в плоскости поперечного сечения плотность тока не изменяется, в результате сложения (5.2) и (5.7) получим уравнение^о/ц1 £(д;)-

- 0-=0, откуда

D 1 d/i

£U)=--

V-n n

Принимая во внимание, что в соответствии с соотношением Эйнштейна В/цп=(()т, где фг - температурный потенциал (фг= =0,025 В при 7=300 К), и полагая, что п=По в начальный момент /=0, окончательно запишем начальное условие

Е(х, =0) = срг

d o (х) dx

(5.12)

Граничные условия. Чтобы задать граничные условия, нужно знать реальное распределение примесей по длине кристалла.