Пусть по(х) изменяется, как показано на рис. 5.4. В структурах реальных диодов нет резких переходов от областей п+ к области По. Кроме того, как видно из рис. 5.4, возможен градиент концентрации доноров в активной области диода, а также выемка (уменьшение по] у катода.

Градиент концентрации примеси наиболее вероятен в коротких диодах (/5 мкм). Выемка может образоваться в том случае, когда активный По-слой диода получен путем эпитакси-ального выращивания на п+-подложке, а второй п+-слой образован при вжигании омического контакта.

Так как на границе активной области диода концентрация примеси По увеличивается до значений 10... Ю' см , то контакты диода по своим электрическим свойствам близки к металлу,т. е. имеют весьма малое сопротивление. Если к диоду приложена разность потенциалов, то падения напряжения на контактах практически нет и напряженность электрического поля близка нулю. Отсюда получаем граничные условия

m )=0, Е(1 0=0, (5.13)

где /д - суммарная длина диода, включающая активную часть и приконт'актные области.

Уравнение (5.11) совместно с условиями (5.12) и (5.13) представляет собой модель диода Ганна. Решая численно уравнение (5.11) с начальным условием (5.12) и граничными условиями (5.13), можно рассчитать функцию Е{х, tk) в дискретные моменты времени tu ti.....tk..... При этом необходимо знать значения внешнего тока в соответствующие моменты времени in{t\), la(2),... ,ia(ft).....По известным функциям Е(х) можно рассчитать напряжение на диоде

Рис. 5.4. Профиль легирования ДГ

а(й)= f Е(Х, h)dx.

(5.14)

Зная а(й), можно рассчитать ток 1 а(*), решая уравнения внешней цепи.

Далее переходим к следующему этапу расчета, вновь обращаясь к уравнению (5.11) и определяя Ыа в момент времени В конечном итоге получаем временные зависимости напряжения на диоде Ua(t) и тока диода ii(t). Кроме того, становится известным распределение поля Е(х) вдоль диода в различные моменты времени. Можно также вычислить распределение концентрации электронов п вдоль диода, решая уравнения (5.9).

Характеристики и параметры модели диода. Для использования модели диода необходимо знать зависимости v{E), По(х), а также параметры й. I, h. Изображенная на рис. 5.3 зависимость V (Е) может быть аппроксимирована выражением

£ \4 , / Е

(5.15)

где Унас = 10 см/с - дрейфовая скорость, соответствующая насыщению характеристики при больших напряженностях поля; £ ==4000 В/см.

Подвижность электронов цп в слабом поле зависит от концентрации доноров По:

(1-Ь/Яда7)

(5.16)

где \ii - подвижность электронов в идеальном беспримесном полупроводнике [для арсенида галлия Цг 8000 см2/(В-с)].

Для арсенида галлия с концентрацией донорных примесей По=2-101...2-101 см-з ц„=5500...8000 см7(В-с), пороговая напряженность поля £пор=3,5 кВ/см, дрейфовая скорость, соответствующая пороговой напряженности поля, Упор= (1,5...2,0)Х XI О' см/с.

Коэффициент диффузии можно вычислить по формуле

(5.17)

где тэ - время релаксации энергии в полупроводнике (для арсенида галлия Тэ Ю-з с).

Следует отметить, что параметры диода Унас, n, D зависят от средней температуры кристалла Т. Зависимости Цп{Т), VaaciT) могут быть аппроксимированы выражениями:

5- (7) = 1 (300/П'. v (T)=v ,A300ir)0.\ (5.18)

Зависимость D{T) может быть рассчитана при подстановке в (5.17) значений ц„(Г) (5.18) и Упор(Г) (5.15).

Границы применимости модели. Распределенная одномерная модель ДГ может быть использована для решения следующих задач:

1) исследования физических процессов в диоде при различных значениях параметров диода;

2) изучения режимов работы диодов в различных схемах автогенераторов на разных частотах;

3) поиска оптимальных параметров диода и внешней цепи.

Границы применимости модели обусловлены принятыми допущениями. Основные из них следующие: 1) средняя дрейфовая скорость электронов v зависит от мгновенного значения напряженности электрического поля Е; 2) коэффициент диффузии D не зависит от напряженности поля Е.

Следует отметить, что первое допущение выполняется не всегда. С ростом частоты колебаний электрическое поле изменяется столь быстро, что скорость электронов не успевает отслеживать эти изменения. Кроме того, требуется определенное время для разгона электронов, в течение которого они приобретают скорость, соответствующую данной мгновенной напряженности поля. Расстояние, которое электроны пролетают за время разгона, должно быть существенно меньше длины диода для того, чтобы можно было считать v функцией мгновенной напряженности поля Е.

Итак, первое допущение ограничивает применимость модели до некоторой граничной частоты (примерно 40 ГГц) и накладывает ограничение на длину активной области диода (/1 мкм). Второе допущение, связанное с постоянством коэффициента диффузии, как показали машинные эксперименты, не приводит к каким-либо заметным ограничениям применимости модели.

Уравнения (5.11) с начальным условием (5.12) и граничным условием (5.13) решаются численно.

§ 5.3. Эквивалентная схема генератора на диоде Ганна

Для решения уравнения, описывающего процессы в ДГ, нужно знать связь мгновенного тока и напряжения на диоде, определяемую внешней цепью. Применяют различные электрические схемы генераторов на диоде Ганна. В § 5.1 отмечалось, что для образования автогенератора на диоде Ганна нет принципиальной необходимости в резонаторе. Простейший генератор состоит из диода, цепи питания и нагрузки (рис. 5.5, а). Здесь приме-

СсЕ

т

Рис. 5.5. Эквивалентные схемы генераторов на ДГ:

с - простейшая схема; б - схема с резонатором

йена параллельная схема питания; Сбл, £бл - элементы, блокирующие источник питания Uo от тока СВЧ; Сев - емкость связи ДГ с нагрузкой Rh-

В режиме стационарных колебаний напряжение на диоде наряду с постоянной составляющей Uo имеет переменную составляющую, образованную падением напряжения на нагрузке при протекании через нее переменного тока ia{t).

Генератор по схеме на рис. 5.5, а на практике применяется редко, поскольку имеет следующие недостатки: 1) форма колебаний ia (t) и ыа (О негармоническая, в результате в нагрузке выделяется мощность не только на основной частоте, но и на ее гармониках; 2) частота колебаний жестко связана с длиной ДГ.

Практика работы с генераторами показала, что КПД по первой гармонике существенно возрастает, если ДГ поместить в резонатор. В случае, когда резонатор в точках подключения диода может быть представлен в виде эквивалентной схемы параллельно соединенных Ci и Li, напряжение на ДГ близко гармоническому. Если же частотная характеристика резонатора подобна характеристике последовательного колебательного контура, то близким гармоническому оказывается ток ДГ. В обоих случаях мощность в нагрузке на гармониках основной частоты ослаблена.

Удобной для моделирования процессов в генераторах на диодах Ганна представляется схема, изображенная на рис. 5.5, б. Изменяя параметры схемы, здесь возможно реализовать режимы с гармонической формой напряжения на диоде, с гармонической формой тока либо промежуточные варианты. Следует отметить, что схема на рис. 5.5, б является эквивалентной, на практике в диапазоне СВЧ применяют резонаторы с распределенными параметрами.

Модель внешней цепи генератора. Модель внешней цепи генератора представляет собой систему алгебраических и обыкновенных дифференциальных уравнений, полученных одним из методов теории линейных цепей (методом переменных состояния, узловых потенциалов и т. п.). Так как модель ДГ позволяет рассчитать напряжение на диоде по известному току, то в модели внешней цепи диод представляется генератором напряжения, управляемым током: Ua(ia).

Для схемы на рис. 5.5, б система алгебро-дифференциальных уравнений, составленных методом переменных состояния, имеет вид

i =uJR , (5.19)

с - - н - il 4~ а>

(5.20) (5.21) (5.22) (5.23)

u=L,uiJut. (5.24)

Эта система решается численно совместно с уравнением (5.11), моделирующим процессы в ДГ. Порядок ее решения следующий.

1. По заданным начальным значениям переменных состояния (напряжений на емкостях и токов нндуктивностей): Ын(о).

hito), iu(to), напряжения источника Uo и напряжения Ыа(/о) вычисляют 1н(о), UL(to), ic{to) в момент времени to путем решения системы алгебраических уравнений (5.19) - (5.21).

2. Решают дифференциальные уравнения (5.22)-(5.24) относительно u {ti), ia{ti), initi) в момент времени ti = to + At, где At - шаг по времени.

3. Происходит обращение к подпрограмме моделирования дг, т. е. численно решают уравнение (5.11) с использованием вычисленного тока диода ia{ti), при этом определяют Е{х, ti) и по (5.14) рассчитывают Ua{ti).

4. Вновь вычисляют /н(1), uiiti) и 1с(Л), решая уравнения (5.19)-(5.21),ит. д.

Процесс вычислений заканчивается, когда в генераторе устанавливается стационарный режим колебаний.

§ 5.4. Режимы работы генераторов на диодах Ганна

Моделирование дг совместно с внешней цепью позволяет проанализировать физические процессы в генераторе при различных параметрах диода и внешней цепи, определяющих режимы его работы. Наибольшее практическое применение имеют два режима, которые характеризуются наибольшими значения-

щ

о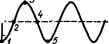

х.пкн

Рнс. 5.6. Результаты моделирования физических процессов в ДГ в пролетном режиме:

о - распределение электрического поля по длине диода в различные моменты времени; б - зависимость напряжения иа диоде от времени; в - зависимость тока диода от времени

МИ ВЫХОДНОЙ МОЩНОСТИ и кпд. в литературе они получили названия: пролетный режим и режим с задержкой образования доменов.

Пролетный режим. Распределение электрического поля в различные моменты времени (/-5), а также формы напряжения а (О и тока ta(0 Диода (полученные путем моделирования

на ЭВМ процессов в схеме на рис. 5.5, б), характерные для пролетного режима, изображены на рис. 5.6. Как видно из рис. 5.6, б, мгновенное напряжение в пролетном режиме всегда больше порогового пор- Это одно из главных условий существования пролетного режима. Из рис. 5.6, а следует, что напряженность электрического поля Е по длине дг распределена неравномерно: имеется область повышенной напряженности £>£пор, в то время как в остальной части дг напряженность поля £вн<£пор. Область повышенной напряженности поля называют дипольным доменом.

Происхождение термина дипольный связано с тем, что область повышенной напряженности поля физически представляет собой двойной заряженный слой (рис. 5.7), как это следует из одномерного уравнения Пуассона (5.11). Отрицательно заряженный слой образуется в результате накопления электронов, а положительно заряженный слой - это область, обедненная электронами, где положительный заряд создают ионизированные доноры.

Из анализа рис. 5.6, с видно, что дипольный домен зарождается у катода и под действием электрического поля перемещается к аноду, где рассасывается. С изменением напряжения Ыа(0 изменяются высота и ширина домена. Следует помнить, что в любой момент времени между напряжением Ыа и напряженностью поля Е существует связь, определяемая (5.14). Нетрудно заметить, что в отдельные моменты времени в дг могут существовать два домена: один, не успевший рассосаться дающийся у катода.

Периодическое зарождение и движение доменов в дг - причина колебаний тока ia (О и напряжения Ыа (О - Период колебаний приближенно определяется временем пролета слоя накопления электронов (левой границы дипольного домена, рис. 5.6, а) от катода к аноду. Электроны в домене находятся под действием поля EEov Как видно из рис. 5.3, их скорость УнасЮ' см/с, поэтому пвриод колебаний в пролетном режиме Тщ,=1/Уаас- Отсюда получасм выражение (5.1) для частоты пролетных колебаний fup-1/Твр-

Таким образом, в пролетном режиме частота колебаний определяется в основном процессами в диоде и слабо зависит от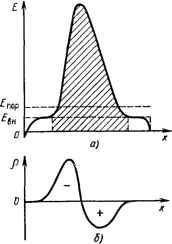

Рис. 5.7. Распределение электрического поля (о) и заряда (б) в ДГ в фиксированный момент времени

на аноде, и новый, зарож-

параметров внешней цепи, которая выделяет первую гармонику из спектра колебаний тока диода *.

Режим с задержкой образования доменов. Распределение поля по длине диода и временные зависимости напряжения и тока диода, характерные для режима с задержкой образования доменов, изображены на рис. 5.8. Кривые, обозначенные цифрами /- 8, соответствуют моментам времени, отмеченным на рис. 5.8, б.

£. кВ/сп

Рис. 5.8. Результаты моделирования физических процессов в ДГ в режиме с задержкой образования доменов:

а - распределение электрического поля по длине диода в различные моменты времени; б - завнсимосгь напряжения на диоде от времени; в - зависимость тока диода от времени

Главная особенность этого режима состоит в том, что часть периода колебаний напряжение на диоде падает ниже порогового. При этом, в отличие от пролетного режима, появляется возможность эффективно управлять частотой колебаний, изменяя параметры внешней цепи.

Действительно, как следует из рис. 5.8, зарождение и движение доменов происходит в диоде лишь в ту часть периода колебаний (промежуток времени 1-6), когда a> iiop. В остальную часть периода (промежуток времени 6-S) поле распределено приблизительно равномерно, причем повсюду £<£пор, поэтому условия для зарождения доменов не выполняются. После рассасывания предыдущего домена на аноде (момент времени 6) новый домен не образуется до тех пор, пока мгновенное напряжение на диоде вновь не превысит пороговое (момент времени 8). Существенно, что задержка образования доменов зависит от параметров внешней цепи генератора (см. рис. 5.5, б), изменяя ко-

* Более детальное изучение процессов в генераторе на ДГ показывает, что внешняя цепь оказывает определенное влияние иа частоту генерации в пролетном режиме (см. § 5.5).

торые можно менять длительность участка 6-8, когда Ыа<Ыпор. и тем самым изменять период колебаний.

Из рис. 5.8 видно, что период колебаний в режиме с задержкой образования доменов больше суммарного времени накопления электронов и пролета слоя накопления через диод. Таким образом, частота колебаний здесь ниже пролетной, определяемой выражением (5.1). Возможен другой вариант режима с задержкой образования доменов, когда время, соответствующее Ыа> > пор (участок 1-6 на рис. 5.8, б), меньше времени пролета домена от катода к аноду. В этом случае в момент времени 6 домен исчезает внутри диода, не достигая анода. Эту разновидность режима в литературе называют режимом с подавлением (или гашением) доменов. В режиме с подавлением доменов частота колебаний оказывается выше пролетной частоты. Расчеты на ЭВМ и практика работы с генераторами показали, что меняя параметры внешней цепи, можно изменять частоту генерации в пределах 0,6/npfl,4fiip.

Следует помнить, что картины распределения поля по длине диода (см. рис. 5.6 и 5.8) получены в предположении неоднородного распределения примесей в ДГ (см. рис. 5.4).

Другие режимы. Известны и другие режимы работы генераторов на диодах Ганна. Один из них называют режимом ограниченного накопления объемного заряда (ОНОЗ). В этом режиме период колебаний, задаваемый внешней цепью, существенно меньше времени пролета слоя накопления электронов от катода к аноду. В результате поле внутри диода равномерно распределяется вдоль длины его активной части /, динамическая вольт-амперная характеристика диода повторяет вид кривой v{E), а частота оказывается не связанной с длиной / и может быть существенно выше fnp. Однако широкого применения данный режим не нашел, что связано с трудностью его реализации. Основная проблема состоит в необходимости подавления паразитных колебаний на частотах, близких пролетной.

В литературе описаны и другие режимы, например двухчас-тотный, режим со стоячим доменом у анода, но их практическое значение пока невелико.

§ 5.5. Обсуждение результатов моделирования

Полученные на ЭВМ результаты моделирования физических процессов в ДГ требуют обсуждения и объяснения. Рассмотрим их некоторые особенности.

Как видно из рис. 5.6 и 5.8, дипольный домен образуется у катода, когда напряженность электрического поля Е>Еаор, т. е. когда мгновенное напряжение на диоде превышает пороговое. Для объяснения причины зарождения доменов предположим, что в начальный момент времени при Ua> nop поле внутри диода

Рис. 5.9. Распределение электрического поля по длине ДГ в начальный момент времени

распределено равномерно, с некоторым градиентом у контактов (рис. 5.9).

Рассмотрим две точки вблизи катода (xi и Хг) на рис. 5.9, где £>£пор. Как видим, напряженность поля Ei<.Ei. В соответствии с рис. 5.3 при £>£пор большей напряженности поля

соответствует меньшая скорость электронов, поэтому скорость в точке Хг меньше скорости в точке Х]. В результате электроны, которые в начальный момент времени находились в точке Хг, несколько отстают, а электроны, стартующие из точки Xi, стремятся их догнать.

Таким образом, у катода образуется слой накопления .электронов - обогащенный слой. В соответствии с законом сохранения количества электричества, если на каком-либо участке цепи накапливается заряд одного знака, то на другом участке должен накапливаться заряд противоположного знака. Как видно из рис. 5.7, положительный заряд образуется справа от обогащенного слоя. Заметим, что такое расположение зарядов характерно лишь для неоднородного распределения примесей по длине диода.

Итак, зарождение домена - прямое следствие существования участка отрицательной крутизны на зависимость v{E) (см. рис. 5.3).

Колебания тока диода. Периодическое образование и движение доменов в ДГ приводит к колебаниям тока диода. Внутри диода существуют токи проводимости, диффузии и смещения, сумма которых равна внешнему току и (5.10). Как видно из рис. 5.7, а, напряженность поля вне домена £вн<£пор, поэтому ток проводимости в этой части диода

крЯрЩпЕ^А- (5.25)

Так как вне домена дЕ/дхаО, то в соответствии с (5.9) = 0 и диффузионный ток равен нулю. Ток смещения вне домена

icn - EaAdETi/dt.

Из анализа рис. 5.6, а и 5.8, а следует, что £вн периодически меняется. Если допустить, что эти изменения происходят по гармоническому закону с частотой / и амплитудой Ет, то амплитуда тока смещения 1сп=ШаАЕт, где сй=2я/. При этом амплитуда тока проводимости /пр=9оЛоЦп/4£т. Отсюда найдем отношение

-=(1,5...2). 10- - .

/см 2яед .

Обычно В ДГ По =(2...4)-105 с/см, поэтому вне домена ток проводимости на порядок выше тока смещения.

пор

Рис. 5.10. Зависимость тока проводимости ДГ от времени в пролетном режиме

Итак, можно считать, что вне домена imiup, где inp определяется выражением (5.25). Так как £вн<£пор, то д.п£вн<Упор и

вн<пор, где 1пор = 9оЛо^пор.

В соответствии с выражением (5.4) суммарный ток не зависит от координаты х. Поэтому в ту часть периода колебаний, когда домен движется от катода к аноду, ток, протекающий через выводы диода, равен току проводимости (5.25).

При рассасывании домена на аноде в случае постоянного напряжения Ыа напряженность поля вн увеличивается до значения пор и соответственно ток проводимости возрастает до значения inop. Таким образом, в процессе образования, движения и рассасывания доменов ток проводимости диода периодически изменяется от Inop до некоторого значения imin<inop (рис. 5.10).

Формирование и рассасывание доменов связано с перераспределением заряда внутри диода. Таким образом, в промежутки времени, соответствующие зарождению и рассасыванию доменов, в полном токе диода возрастает ток смещения.

Так как домен состоит из двух слоев с зарядами противоположных

знаков, то его можно уподобить некоторому конденсатору емкостью Сд- Тогда ток смещения равен току заряда этого конденсатора: icw=Cg(ug)uuglut, где Ug - напряжение на домене (площадь заштрихованной области на рис. 5.7, с). Как видно из рис. 5.7, а, ugfuua, где Иа определяется выражением (5.14). Поэтому

i, Cd(u,)duJut. (5.26)

В зависимости от формы напряжения Ыа(0 ток tcM может быть различным. Если крутизна зависимости Ua(t) велика, то значительным оказывается ток смещения и суммарный ток диода может быть существенно выше Inop (см. рис. 5.8, в).

Временные зависимости напряжения на диоде. Колебания напряжения на диоде образуются при протекании периодически меняющегося тока ia(t) через внешнюю цепь. Форма колебаний напряжения определяется сопротивлением внешней цепи на частоте колебаний и ее гармониках, а также спектральным составом тока. Как видно из рис. 5.6, с, форма напряжения в пролетном режиме близка гармонической. Это означает, что в данном случае сопротивление внешней -цепи генератора (см. рис. 5.5, б) велико на основной частоте и мало на гармониках (мала индуктивность L). Следует отметить, что в пролетном режиме возможна и негармоническая форма Ыа (t) при соответствующем выборе параметров внешней цепи.

в режиме с задержкой образования доменов, как показало моделирование на ЭВМ, форма напряжения всегда негармоническая (имеется уплощение при Ыа< пор). Это объясняется тем, что при Ыа< пор диод эквивалентен небольшому сопротивлению Ro. шунтирующему колебательную систему и снижающему ее добротность.

Следует отметить, что негармоническая форма Ыа (t) (см. рис. 5.8, б) способствует увеличению КПД по первой гармонике. Для реализации указанной формы и^Ц) на практике необходимо, чтобы внешняя цепь обладала высоким входным сопротивлением на гармониках основной частоты (должна быть достаточно большой индуктивностью L в схеме на рис. 5.5, б).

Период колебаний. Изучение рис. 5.6 и 5.8 позволяет сделать следующие выводы: домен образуется при Ua nop, при этом ia>inop; домен задерживается у катода до тех пор, пока ток диода не упадет ниже значения inop-

В пролетном режиме период колебаний складывается из времени задержки домена у катода и времени пролета обогащенного слоя через активную область диода. Время задержки зависит от формы тока ia(t), которая в значительной мере определяется формой напряжения Ua{t), а последняя, в свою очередь, зависит от входного сопротивления резонатора. В результате изменение параметров внешней цепи приводит к некоторому изменению периода колебаний.

В режиме с задержкой образования доменов период колебаний равен сумме трех временных интервалов: времени задержки домена у катода (участок /-3 на рис. 5.8); времени пролета обогащенного слоя через диод (участок 3-6); времени задержки образования домена (участок 6-8). Как видим, здесь частота генерации управляется не только током (как в пролетном режиме), но и напряжением, поэтому диапазон изменения частоты существенно выше.

§ 5.6. Оптимальные параметры диода Ганна

Моделирование физических процессов в ДГ, включенном в схему автогенератора, позволяет найти оптимальные значения электрофизических и конструктивных параметров диода. Критерием оптимальности обычно считают максимум КПД т]= =Рвых/Ро, где Рвых - выходная мощность; Ро - мощность, потребляемая от источника питания.

В процессе изготовления ДГ можно изменять следующие параметры: среднюю концентрацию донорных примесей По и ее распределение по длине диода ДЛо/ о; длину активной части диода / и площадь сечения А.

Подвижность цп и коэффициент диффузии D постоянны для конкретной технологии выращивания кристаллов арсенида галлия и зависят от концентрации неконтролируемых примесей.

Желательно, чтобы подвижность электронов ц„ была по возможности большей. При больших цп увеличивается пороговая скорость ynopixnnop и, следовательно, возрастает отношение ь'пор/Унас (см. рис. 5.3), ЧТО приводит К уменьшению электрического параметра диода m=/min/inop и соответствующему росту КПД.

В одной из ранних работ по исследованию генератора на ДГ на ЭВМ получено оптимальное соотношение для произведения По1 (см-2): /го/= (1...2) 102, причем предполагалось, что концентрация По распределена по длине диода равномерно, а напряжение на диоде имеет гармоническую форму.

В более поздних работах показано, что для увеличения КПД при несинусоидальных формах Ыа(0 целесообразно увеличивать произведение По1. Однако с увеличением о/ растет температура диода, соответственно увеличивается параметр т и снижается

КПД. В настоящее время в качестве оптимального принято считать соотношение

V=(2...4)-10 2 см-2. (5.27)

Соотношение (5.27) совместно с выражением (5.1) являются основными для разработчиков ДГ и позволяют изготовлять оптимальные приборы для разных частотных диапазонов.

Из выражений (5.27) и (5.1) вытекает требование к средней

о

20 <-0 йПо v S)

Рис. 5.11. Равномерный про- Рис. 5.12. Зависимость электронного КПД филь легирования ДГ (а) и (а) и выходной мощности (б) генератора соответствующее ему распреде- на ДГ от неравномерности легирования ление электрического поля по длине диода в различные моменты времени (б)

концентрации примесей По (см~) для диодов на разные частотные диапазоны: По= (2...4) 10 f, где f - в Гц.

Влияние на КПД неравномерности распределения примесей по длине диода. Моделирование на ЭВМ процессов в ДГ с использованием модели, описанной в § 5.3, дает возможность про-

анализировать влияние неравномерности распределения По по длине диода на его режим работы и выходные параметры генератора Ганна.

На рис. 5.11 изображен равномерный (без выемки и градиента) профиль легирования и соответствующие ему картины распределения поля в различные моменты времени (/-5) для схемы генератора на ДГ, показанной на рис. 5.5, б. Из уравнения Пуассона следует, что в данном случае в активной области ДГ имеется движущийся отрицательно заряженный слой, обогащенный электронами, а компенсирующий его положительный заряд расположен в аноде.

На рис. 5.12 представлены зависимости КПД и выходной мощности генератора на ДГ от значения ДПо/по, где Дпо =

= Отах- Omln; О = ( О max-f О mln)/2 (СМ. рИС. 5.4). ЭтИ ЗаВИ-

симости получены В. К. Копаенко и Т. М. Шарифовым в результате моделирования на ЭВМ физических процессов в генераторе, выполненном по схеме на рис. 5.5, б, с использованием модели ДГ, описанной в § 5.2, и модели внешней цепи, описанной в § 5.3; длина активной области / ДГ составляла 10 мкм. Как видим, имеется оптимальное значение Дпо/по, примерно равное 20% для диода с /=10 мкм.

В заключение приведем типичные параметры ДГ и генераторов на их основе. Диапазон частот ДГ 1...100 ГГц; выходные мощности в непрерывном режиме работы единицы ватт - единицы милливатт, в импульсном режиме - десятки ватт; КПД в непрерывном режиме 1...5%, в импульсном - 5...10%. Наибольший КПД получается в режиме с задержкой образования доменов. Особенностью генераторов на диодах Ганна является возможность существенного (примерно на порядок) увеличения выходной мощности при переходе от непрерывного к импульсному режиму (при длительности импульсов, меньшей 1 мкс).

ГЛАВА 6

ПРОЕКТИРОВАНИЕ ДИОДНЫХ АВТОГЕНЕРАТОРОВ СВЧ

§ 6.1. Квазилинейная теория диодных автогенераторов

должны удовлетворять следующим

Автогенераторы СВЧ требованиям:

генерировать на частоте /о мощность не меньше заданной выходной мощности Рвых;

иметь КПД, близкий максимальному;

обеспечивать заданную стабильность частоты Д /о и выходной мощности ДРвых/Рвых;

иметь низкий уровень шумов;

стационарный режим колебаний должен быть устойчив в диапазоне климатических, механических и фоновых внешних воздействий;

не должно быть паразитных колебаний.

Помимо перечисленных основных требований к автогенераторам различного типа предъявляют иногда и дополнительные требования:

возможность механической, электрической или магнитной перестройки частоты;

возможность стабилизации частоты высокодобротным резонатором или синхронизации частоты от внешнего высокостабильного источника;

сопрягаемость с другими устройствами радиосистемы и др.

Чтобы учесть все требования к АГ, представляется целесообразным дополнить изложенные в гл. 5 машинные методы проектирования простой аналитической теорией.

Стационарный режим автоколебаний. Автогенератор можно представить в виде эквивалентной схемы (рис. 6.1, с), содержащей активный элемент (АЭ), колебательную систему и сопротивление нагрузки. В соответствии с квазилинейной теорией не интересуются наличием высших гармоник в составе спектра напряжения и тока диода, а принимают во внимание лишь основную частоту колебаний. Кристалл генераторного диода

Колебательная система

J

Рис. 6.1. Эквивалентные схемы диодных автогенераторов:

о - обобщенная схема; б - схема, в которой диод и внешняя цепь представлены проводим ост ям и

моделируют усредненной по первой гармонике комплексной проводимостью Ya==Iai/Uau где Оаи hi - комплексные амплитуды первой гармоники напряжения и тока диода.

Действительные и мнимые части Уа - функции амплитуды колебаний: lfa(t/ai) = -Ga(t/ai)-f jjBa(t/ai). Колсбательная система АГ, независимо от числа резонаторов, описывается ее проводимостью Кк относительно точек подключения кристалла диода (рис. 6.1). Поскольку внешняя цепь генераторов линейна, то ?к не зависит от амплитуды, а зависит только от частоты:

Следует отметить, что проводимость ?а также зависит от частоты, однако, учитывая, что эта зависимость обычно более слабая, чем 5к((о), для простоты ею пренебрегают.